前言

之前看了labuladong的二分模版，以为自己懂了，结果遇到题目还是到处吃瘪，各种细节直接痛苦面具放弃思考 😭

最近看到一个讲二分查找的视频，感觉我又行了！特此记录一下该方法，主要思想就是：把红蓝区域固定，然后通过选择返回的r，l获得上界和下界，这样取区域与返回值可以更加灵活多变。

比如在一段集合里 [1,2,3,5,5,5,8,9] 可以有四种情况，要如何进行二分的设计？

找到第一个 >=5 的元素
找到最后一个<5 的元素
找到第一个 >5 的元素
找到最后一个 <=5 的元素

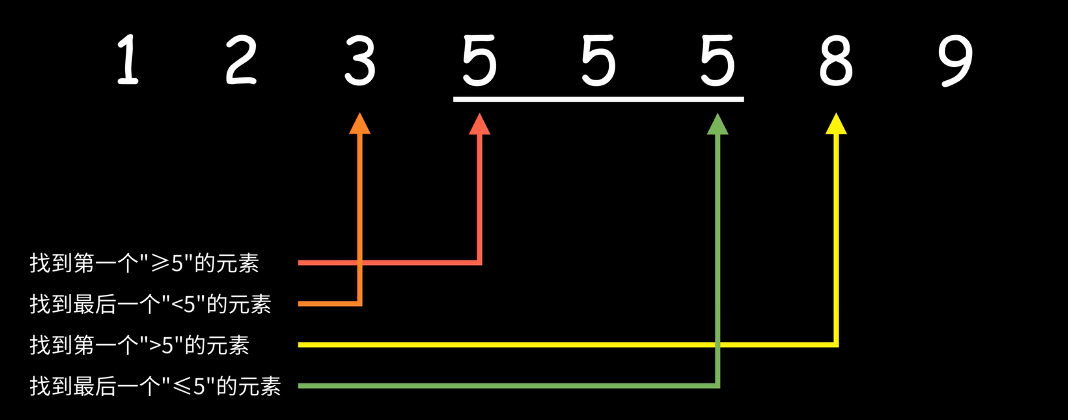
「二分」的本质是两段性，并非单调性。只要一段满足某个性质，另外一段不满足某个性质，就可以用「二分」。

算法流程

对于一个数组，可以将二分查找任务转换为寻找其 蓝红边界 ，即求出未知数K-1和K的位置。（target=5）

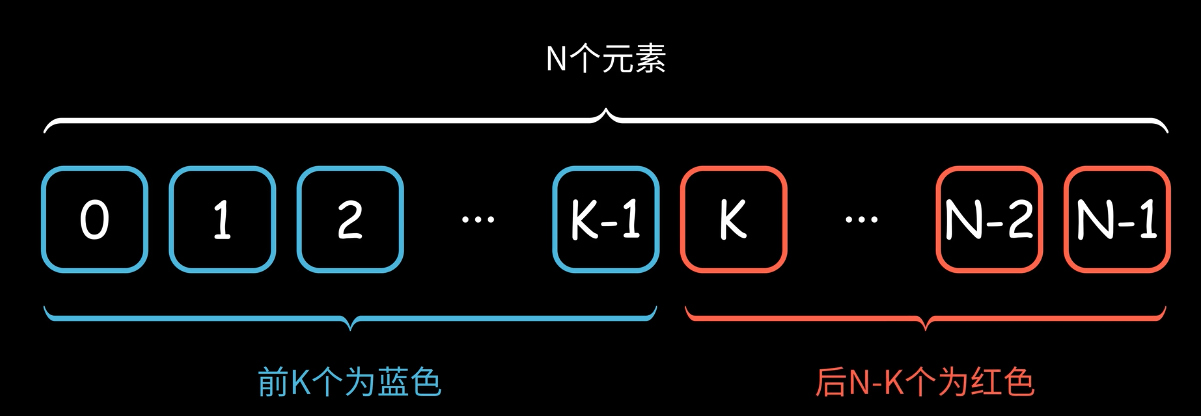
1）首先整个数组都是灰色的，蓝红指针为别初始化位-1和数组长度length。首先查看数组最中间的元素 4 为蓝色，所以将蓝色边界直接扩展到该元素所在位置。

2）继续上述步骤，观察灰色区域中最中间的元素 6 为红色，所以将红色指针扩展到该元素所在的位置。

3）一直重复执行上述操作，最后就能够找到蓝红边界：

伪代码

初始：l 指向蓝色区域， r 指向红色区域
循环： l 、 r 快速向蓝红边界逼近，并保持 l 、 r 颜色不改变
结束： l 、 r 刚好指向蓝红边界

l = -1, r = N // 首先初始化两个指针，l指向-1，r指向数组长度N
while (l+1 ！= r){ // 循环直至l+1 = r
  m = (l+r)/2 // 求出灰色数组中间元素的位置，并向下取整（注意溢出）
  if isBlue(m) l = m // 如果l的颜色为蓝色，就把蓝色区域拓展到m (把 m 赋值给 左指针)
  else r = m // 否则红色区域扩展到m (把m赋值给右指针)
}
return l or r  // 此时的l和r刚刚好指向蓝红边界，可以根据实际情况返回l还是r

防止溢出：

if(x == Integer.MAX_VALUE){
  m = (right+left)/2;
}else{
  m = (right-left)/2+left;
}
// 或者直接用long接收 然后转换为int
Integer.parseInt(String.valueOf(m))

查找元素不存在怎么办

因为left指针始终在right指针之后，查找上界时会存在三种情况（此时返回的是right指针）：

[5,6,8,8,9] target = 1 => right = 0 （此时nums[right]!=target）
[5,6,8,8,9] target = 10 => right = nums.length（越界了）
[5,6,8,8,9] target = 7 => right = 2 (如果target在数组中的话，会返回刚好大于target的值。同样的，此时nums[right]!=target)

int left = -1;
int right = nums.length;

while (left + 1 != right) {
  int m = (left + right) / 2;
  if (nums[m]<target){
    left = m;
  }else {
    right=m;
  }
}
if (right==nums.length||nums[right]!=target){
  right = -1;
}
return right;

查找下界时，返回的left指针，同样也是三种情况：

[5,6,8,8,9] target = 1 => left = -1 （越界了）
[5,6,8,8,9] target = 10 => left = nums.length-1（此时nums[right]!=target）
[5,6,8,8,9] target = 7 => left = 1 (如果target在数组中的话，会返回刚好小于target的值。同样的，此时nums[right]!=target)

int left = -1;
int right = nums.length;

while (left + 1 != right) {
  int m = (left + right) / 2;
  if (nums[m]<=target){
    left = m;
  }else {
    right=m;
  }
}

if (left==-1||nums[left]!=target){
  left=-1;
}
return left;

细节问题

细节1：为什么 l 的初始值为-1 ，r 的初始值为 N

当l初始化为0的情况下，如果整个数组都是红色，l一开始则会落于红色区域内。r初始化为N-1同理。

细节2：m 是否是种处于[0,N)的左闭右开区间以内

只有m属于[0,N)的左闭右开区间以内，isBlue(m) 判断颜色才是有意义的。

先来看m的下界：因为 m = (l+r)/2, 只要让l、r尽可能的小即可。l的最小值即为他的初始值-1，对于r 而言，如果他能进入循环体，他的最小值为1。因此m的最小值即为 (-1+1)/2=0。

再来看m的上界：要让l、r尽可能的大即可，r 的最大值为 N， l 则为N-2 ， m 的最大值则为 N-1。

因此 m 始终处于于[0,N)的左闭右开区间以内，即m不会溢出。

细节3：更新指针的时候，能不能写成 l = m +1 或者 r = m - 1

对于下图的情况，在某次循环中m刚刚好指向蓝色区域的最后一个元素，如果 l = m +1 就会让l指向红色区域造成了错误。 r = m - 1同理。

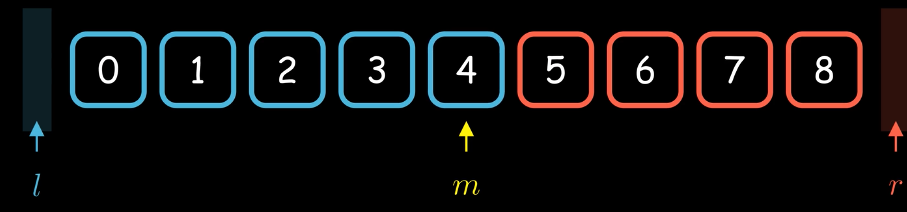
细节4：程序会不会陷入死循环

无论l和r 之间隔了多少个元素，都一定会退化到第一种情况并退出循环。

总结

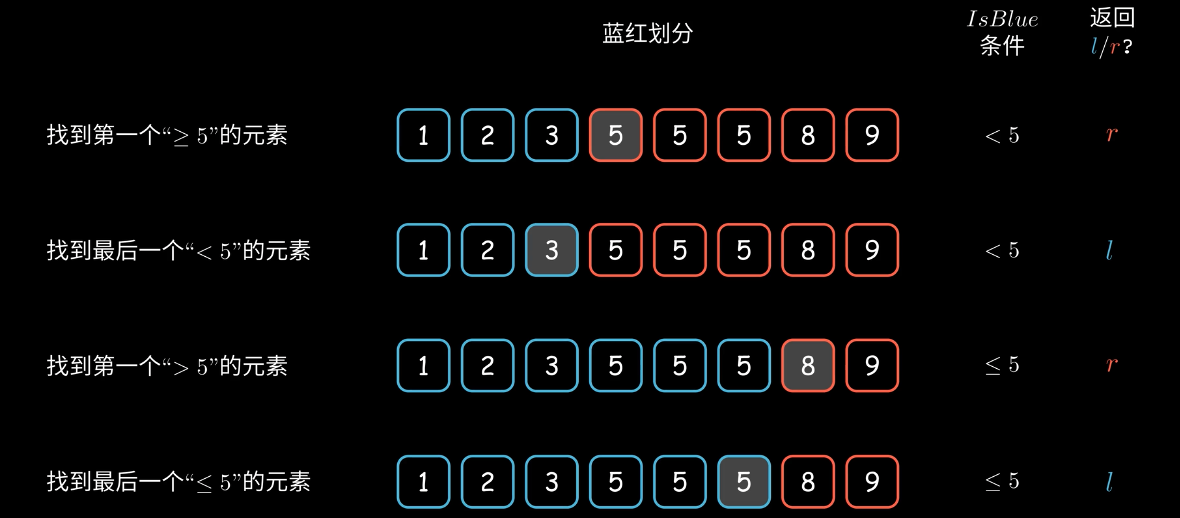
对于前言中的问题，结合以上分析可归纳出二分查找设计的一般流程：

建模：划分蓝红区域，确定 isBlue()函数的条件
确定返回l 还是 r
套用伪代码模版
如果有需要则加入一下预处理或后处理逻辑

// case0: 单纯的查找target的下标(无重复元素)，不存在返回-1
private int binarySearch(int[] arr,int target) {
  int left = -1;
  int right = arr.length;

  while (left+1!=right){
    int m = (right-left)/2 + left; // 因为left=-1，所以还是可能会溢出
    if (arr[m]<=target){
      left = m;
    }else {
      right = m;
    }

  }

  // 不存在的情况
  if (left==-1||arr[left]!=target){ // 单纯无重复元素的查找还需要考虑元素在数组中但是不相等的情况
    left = -1;
  }

  return left;
}


// case1: 寻找第一个 >=target 的元素的下标，不存在返回-1 (找下界)
private int binarySearch(int[] arr,int target) {
  int left = -1;
  int right = arr.length;

  while (left+1!=right){
    int m = (right-left)/2 + left; // 因为left=-1，所以还是可能会溢出
    if (arr[m]<target){
      left = m;
    }else {
      right = m;
    }

  }

  // 不存在的情况
  if (right==arr.length){
    right = -1;
  }

  return right;
}
// case2: 寻找最后一个 <target 的元素的下标，不存在返回-1
private int binarySearch(int[] arr,int target) {
  int left = -1;
  int right = arr.length;

  while (left+1!=right){
    int m = (right+left)/2;
    if (arr[m]<target){
      left = m;
    }else {
      right = m;
    }

  }
  // 不存在的情况
  if (left==-1){
    left = -1;
  }

  return left;
}
// case3: 寻找第一个 >target 的元素的下标，不存在返回-1
private int binarySearch(int[] arr,int target) {
  int left = -1;
  int right = arr.length;

  while (left+1!=right){
    int m = (right+left)/2;
    if (arr[m]<=target){
      left = m;
    }else {
      right = m;
    }

  }
  // 不存在的情况
  if (right==arr.length){
    right = -1;
  }

  return right;
}
// case4: 寻找最后一个 <=target 的元素的下标，不存在返回-1  (找上界)
private int binarySearch(int[] arr,int target) {
  int left = -1;
  int right = arr.length;

  while (left+1!=right){
    int m = (right+left)/2;
    if (arr[m]<=target){
      left = m;
    }else {
      right = m;
    }

  }
  // 不存在的情况
  if (left==-1){
    left = -1;
  }

  return left;
}

刷题时间

69. x 的平方根

题目

实现 int sqrt(int x) 函数。
计算并返回 x 的平方根，其中 x 是非负整数。
由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:
输入: 4
输出: 2

解析

返回类型是只保留整数部分，那么不就是要我们找到 $mid<=\sqrt{x}$的上界吗

扩大蓝色的条件：m*m<=x 都属于蓝色
返回l

public int mySqrt(int x) {
  if (x==0) return 0;
  if (x==1) return 1;

  int left = -1;
  int right = x;
  int m = 0;

  while (left+1!=right){
    if(x == Integer.MAX_VALUE){
      m = (right+left)/2;
    }else{
      m = (right-left)/2+left;
    }
    
    if ((long)m*m<=x){
      left = m;
    }else {
      right = m;
    }

  }
  return left;
}

278. 第一个错误的版本

题目

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例:
给定 n = 5，并且 version = 4 是第一个错误的版本。
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。 

解析

找到第一个true：

扩大蓝色的条件：m= flase (表示错误的版本)
返回right

0---------------first--------------N
      mid       mid       mid
     false      true      true

public int firstBadVersion(int n) {
  long left = -1;
  long right = (long)n+1;

  while(left+1!=right){
    long m = (right-left)/2+left;
    if(isBadVersion(Integer.parseInt(String.valueOf(m)))==false){
      left = m;
    }else{
      right=m;
    }
  }
  return Integer.parseInt(String.valueOf(right));
}

34. 在排序数组中查找元素的第一个和最后一个位置

题目

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target，返回 [-1, -1]。
进阶：
你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？
 
示例 1：
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]
示例 2：
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

解析

查找元素的第一个位置： [5,7,7,8,8,9] target=8

扩大蓝色的条件：nums[m]<8
返回right
注意不存在的场景：right==nums.length||nums[right]!=target

查找元素的最后一个位置：

扩大蓝色的条件：nums[m]<=8
返回left
注意不存在的场景：left==-1||nums[left]!=target

public int[] searchRange(int[] nums, int target) {
  int[] res = new int[2];

  // 找上界
  int left = -1;
  int right = nums.length;

  while (left + 1 != right) {
    int m = (left + right) / 2;
    if (nums[m]<target){
      left = m;
    }else {
      right=m;
    }
  }
  if (right==nums.length||nums[right]!=target){
    res[0] = -1;
  }else {
    res[0] = right;
  }


  // 找下界
  left = -1;
  right = nums.length;

  while (left + 1 != right) {
    int m = (left + right) / 2;
    if (nums[m]<=target){
      left = m;
    }else {
      right=m;
    }
  }

  if (left==-1||nums[left]!=target){
    res[1] = -1;
  }else {
    res[1] = left;
  }

  return res;
}

153.寻找旋转排序数组中的最小值 ⭐️

题目

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]]。
给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素。

示例 1：
输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。
示例 2：
输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

解析

「二分」的本质是两段性，并非单调性。只要一段满足某个性质，另外一段不满足某个性质，就可以用「二分」。
经过旋转的数组，显然前半段满足 >= nums[0]，而后半段不满足 >= nums[0]。我们可以以此作为依据来划分蓝红区间。
扩大蓝色的条件：nums[m]>= nums[0]
返回right

public int findMin(int[] nums) {
  int left = -1;
  int right = nums.length;

  while (left+1!=right){
    int m = (right-left)/2+left;

    if (nums[m]>=nums[0]){ // 记得有=号，特殊case[2,1]
      left = m;
    }else {
      right = m;
    }
  }

  if (right==nums.length) return nums[0]; // 旋转了一圈回来了,如[1,2,3,4]

  return nums[right];
}

154.寻找旋转排序数组中的最小值 II ⭐️

题目

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]
注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个可能存在 重复 元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

示例 1：
输入：nums = [1,3,5]
输出：1
示例 2：
输入：nums = [2,2,2,0,1]
输出：0
  
提示：
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

解析

不同的是，本题元素并不唯一。
这意味着我们无法直接根据与 nums[0] 的大小关系，将数组划分为两段，即无法通过「二分」来找到旋转点。因为「二分」的本质是二段性，并非单调性。只要一段满足某个性质，另外一段不满足某个性质，就可以用「二分」。
但如果旋转点使得相同元素进行了分裂将会失去两段性，如[01222345] =>[23450122]。我们需要做一些预处理操作，使得其二段性恢复方便我们通过「二分」找旋转点。我们可以将新数组尾部与nums[0]相同的元素忽略使得其二段性恢复。
预处理：删除数组末尾上所有与nums[0]相同的数，即把right指针指到最后一个等于nums[0]的数。然后继续划分红蓝区间：
扩大蓝色的条件：nums[m]>= nums[0]
返回right ,即旋转点(最小数的下标+1)

public int findMin(int[] nums) {
  int left = -1;
  int right = nums.length;

  while (right>1 && nums[0] == nums[right-1]) right--; // 防止把所有数都删光了

  while (left+1!=right){
    int m = (right-left)/2+left;

    if (nums[m]>=nums[0]){
      left = m;
    }else {
      right = m;
    }
  }

  if (right==nums.length) return nums[0];

  return nums[right];
}

33.搜索旋转排序数组

题目

整数数组 nums 按升序排列，数组中的值 互不相同 。
在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1：
输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4
示例 2：
输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1
示例 3：
输入：nums = [1], target = 0
输出：-1

解析

先找到「153. 寻找旋转排序数组中的最小值」的索引，由此可以将数组分为升序的两段。
根据 nums[0] 与 target 的关系判断 target 在左段还是右段，再对升序数组进行二分查找即可。

public int search(int[] nums, int target) {
  int index = findMin(nums); // 旋转点
  int left = 0;
  int right = 0;

  // 根据 nums[0] 与 target 的关系判断 target 在左段还是右段，再对升序数组进行二分查找即可。
  // [4,5,6,7,0,1,2]
  if (target>=nums[0]){ 
    // target 在左段
    left = -1;
    right = index;
  }else {
    // target 在右段
    if (index==nums.length){
      left = -1;
    }else {
      left = index-1;
    }

    right = nums.length;
  }

  // 二分查找target，无重复元素
  while (left+1!=right){
    int m = (right-left)/2+left;
    if (nums[m]<=target){
      left= m;
    }else {
      right = m;
    }
  }

  if (left==-1||nums[left]!=target){
    left=-1;
  }

  return left;

}

// 返回旋转数组的最小值下标
public int findMin(int[] nums) {
  int left = -1;
  int right = nums.length;

  while (left+1!=right){
    int m = (right-left)/2+left;

    if (nums[m]>=nums[0]){ // 记得有=号，特殊case[2,1]
      left = m;
    }else {
      right = m;
    }
  }

  if (right==nums.length) return right; // 旋转了一圈回来了,如[1,2,3,4]。返回的下标不是值

  return right;
}

81. 搜索旋转排序数组 II

题目

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。
在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

示例 1：
输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true
示例 2：
输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

解析

预处理恢复二段性：删除数组末尾上所有与nums[0]相同的数，即把right指针指到最后一个等于nums[0]的数。
先找到「153. 寻找旋转排序数组中的最小值」的索引，由此可以将数组分为升序的两段。
根据 nums[0] 与 target 的关系判断 target 在左段还是右段，再对升序数组进行二分查找即可。

public boolean search(int[] nums, int target) {
  int index = findMin(nums); // 旋转点
  int left = 0;
  int right = 0;

  // 根据 nums[0] 与 target 的关系判断 target 在左段还是右段，再对升序数组进行二分查找即可。
  // [4,5,6,7,0,1,2]
  if (target>=nums[0]){
    // target 在左段
    left = -1;
    right = index;
  }else {
    // target 在右段
    if (index==nums.length){
      left = -1;
    }else {
      left = index-1;
    }

    right = nums.length;
  }

  // 二分查找target，无重复元素
  while (left+1!=right){
    int m = (right-left)/2+left;
    if (nums[m]<=target){
      left= m;
    }else {
      right = m;
    }
  }

  if (left==-1||nums[left]!=target){
    return false;
  }

  return true;

}

// 返回旋转数组的最小值下标
public int findMin(int[] nums) {


  int left = -1;
  int right = nums.length;

  // 预处理恢复二段性
  while (right>1&&nums[0]==nums[right-1]) right--;


  while (left+1!=right){
    int m = (right-left)/2+left;

    if (nums[m]>=nums[0]){ // 记得有=号，特殊case[2,1]
      left = m;
    }else {
      right = m;
    }
  }

  if (right==nums.length) return right; // 旋转了一圈回来了,如[1,2,3,4]

  return right;
}

162. 寻找峰值 ⭐️

题目

峰值元素是指其值大于左右相邻值的元素。
给你一个输入数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。 // 这就代表着 只要数组中存在一个元素比相邻元素大，那么沿着它一定可以找到一个峰值

示例 1：
输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。
示例 2：
输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；或者返回索引 5， 其峰值元素为 6。

解析

这题看着复杂，其实挺简单，他的两段性在数据中，我们可以找：

上升区域的上界，上升区域必然有nums[mid]>nums[mid-1]
下降区域的下界，下降区域必然有nums[mid]>nums[mid+1]
当然还需要考虑mid在两侧的情况，这里我们选第一种做法吧。

        /\
   /\  /  \
\ /  \/    \
            \
public int findPeakElement(int[] nums) {
  int left = -1;
  int right = nums.length;

  while (left+1!=right){
    int m = (right-left)/2+left;
    if (m==0||nums[m]>nums[m-1]){ // m==0 保证有进场资格
      left = m;
    }else {
      right = m;
    }
  }
  return left;
}

658. 找到 K 个最接近的元素

题目

给定一个排序好的数组 arr ，两个整数 k 和 x ，从数组中找到最靠近 x（两数之差最小）的 k 个数。返回的结果必须要是按升序排好的。
整数 a 比整数 b 更接近 x 需要满足：
|a - x| < |b - x| 或者
|a - x| == |b - x| 且 a < b

示例 1：
输入：arr = [1,2,3,4,5], k = 4, x = 3
输出：[1,2,3,4]
示例 2：
输入：arr = [1,2,3,4,5], k = 4, x = -1
输出：[1,2,3,4]

解析

这题其实就是找到距离target最接近的元素，即找 >=target的下界的索引。然后向两边扩散找出k个数。

public List<Integer> findClosestElements(int[] arr, int k, int x) {
  ArrayList<Integer> res = new ArrayList<>();

  // 二分找到 >=x 的下界
  int left = -1;
  int right = arr.length;
  while (left+1!=right){
    int m = (right-left)/2+left;
    if (arr[m]<x){
      left = m;
    }else {
      right = m;
    }
  }

  // 此时right为刚好小于等于x的数的下标
  left = right-1;

  while (res.size()!=k){
    if (right==arr.length||left>=0&&Math.abs(x-arr[left])<=Math.abs(arr[right]-x)){
      res.add(0,arr[left]);
      left--;
    }else if (right<arr.length){
      res.add(arr[right]);
      right++;
    }
  }
  return res;
}

744. 寻找比目标字母大的最小字母

题目

给你一个排序后的字符列表 letters ，列表中只包含小写英文字母。另给出一个目标字母 target，请你寻找在这一有序列表里比目标字母大的最小字母。
在比较时，字母是依序循环出现的。举个例子：
如果目标字母 target = 'z' 并且字符列表为 letters = ['a', 'b']，则答案返回 'a'
 
示例：
输入:
letters = ["c", "f", "j"]
target = "a"
输出: "c"
输入:
letters = ["c", "f", "j"]
target = "c"
输出: "f"

解析

蓝色区域包含所有小于等于target的字符

public char nextGreatestLetter(char[] letters, char target) {

  int left = -1;
  int right = letters.length;

  while (left+1!=right){
    int m = (right-left)/2+left;
    if (letters[m]<=target){
      left = m;
    }else{
      right = m;
    }
  }

  return right==letters.length?letters[0]:letters[right]; //如果没有找到就返回第一个字符
}

167. 两数之和 II - 输入有序数组

题目

给定一个已按照 升序排列  的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ，所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length。
你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

示例 1：
输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
示例 2：
输入：numbers = [2,3,4], target = 6
输出：[1,3]

解析

在数组中找到两个数，使得它们的和等于目标值，可以首先固定第一个数，然后寻找第二个数，第二个数等于目标值减去第一个数的差。利用数组的有序性质，可以通过二分查找的方法寻找第二个数。为了避免重复寻找，在寻找第二个数时，只在第一个数的右侧寻找。

public int[] twoSum(int[] numbers, int target) {

  for (int i = 0; i < numbers.length; i++) {
    int left = i;
    int right = numbers.length;

    while (left+1!=right){
      int m  = (right-left)/2+left;
      if (numbers[m]<target-numbers[i]){
        left = m;
      }else {
        right = m;
      }
    }

    if (right==numbers.length||numbers[right]!=target-numbers[i]){
      continue;
    }
    return new int[]{i+1,right+1};
  }
  return new int[]{-1,-1};
}

我再也不怕写错二分查找啦（大概