二叉树
二叉树的分类
满二叉树
它们在顺序存储方式下可以复原
满二叉树的定义
一棵深度为 k 且有 $2^k-1$ 个节点的二叉树成为 满二叉树。
满二叉树的特点
- 每一层上的节点数都是最大节点数,即每层都满
- 叶子结点全部在最底层
满二叉树的编号
- 编号规则:从根结点开始,自上而下,自左而右
- 每一节点位置都有元素
例子
下面是一棵深度为 4 ,有$2^4-1=15$ 个节点的满二叉树。
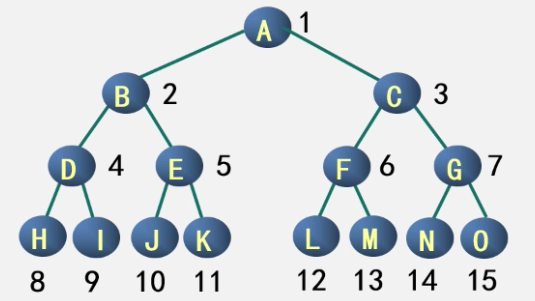
完全二叉树
它们在顺序存储方式下可以复原
完全二叉树的定义
深度为 k 的具有 n 个节点的二叉树,当且仅当其每一个节点都与深度为 k 的满二叉树中编号为 1~n 的节点 一一对应时,称之为 完全二叉树。
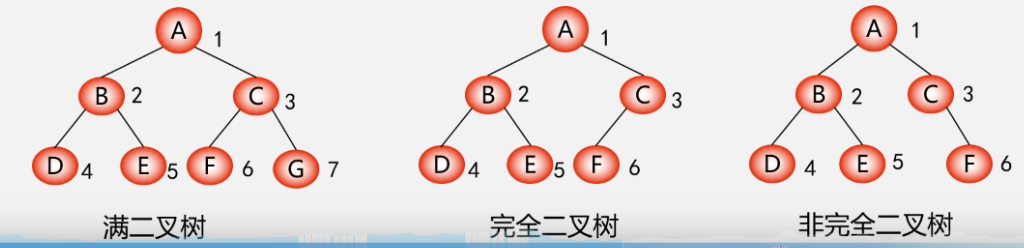
ps:在满二叉树中,从最后一个节点开始,连续去掉任意个节点,即是一棵完全二叉树。
完全二叉树的特点
- 叶子结点只可能分布在层次最大的两层上
- 对任一节点,如果其右子树的最大层次为 i ,则其左子树的最大层次必为 i 或 i+1
二叉查找树/二叉排序树/二叉搜索树
二叉排序树(BST,Binary Sort Tree)的性质:
- 有非叶子结点至多拥有两个儿子(Left和Right);
-
所有结点存储一个关键字;
- 对于二叉树中的任意节点,如果它有左子树或右子树,则该节点的数据成员大于左子树所有节点的数据成员,且小于右子树所有节点的数据成员。
- 排序二叉树的中序遍历结果是从小到大排列的。
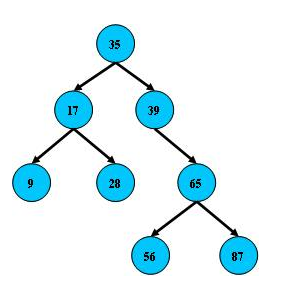
平衡二叉树
平衡二叉树的定义
也被称为AVL树(Adelson-Velskii and Landis),一棵平衡二叉树可以是空树,也可以是具有下列性质的二叉排序树:
- 左子树与右子树的高度之差的绝对值小于等于1
- 左子树和右子树也是平衡二叉排序树
平衡因子
为了方便起见,给每个节点附加一个数字,给出该节点左子树与右子树的高度差。这个数字称为节点的平衡因子BF. \(平衡因子 = 节点左子树的高度 - 节点右子树的高度\) 根据平衡二叉树的定义,平衡二叉树上所有节点的平衡因子只能是-1、0或1。
对于一棵有 n 个节点的AVL树,其高度保持在 $O(log_2n)$ 数量级,ASL也保持在 $O(log_2n)$ 数量级。
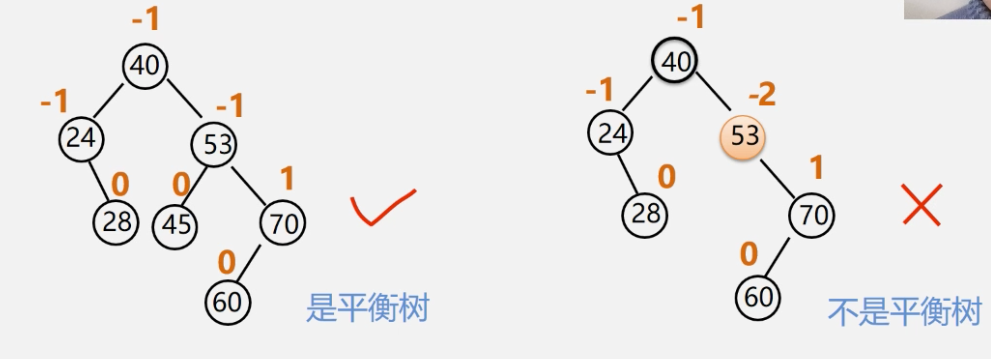
B树(B_树)和B+树:
B树(B-树)
B树也称B-树,它是一颗多路平衡查找树,B树的定义:
- 每个节点最多有m-1个关键字(可以存有的键值对)。
- 根节点最少可以只有1个关键字。
- 非根节点至少有m/2个关键字。
- 每个节点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
- 所有叶子节点都位于同一层,或者说根节点到每个叶子节点的长度都相同。
- 每个节点都存有索引和数据,也就是对应的key和value。
所以,根节点的关键字数量范围:1 <= k <= m-1,非根节点的关键字数量范围:m/2 <= k <= m-1。
另外,我们需要注意一个概念,描述一颗B树时需要指定它的阶数,阶数表示了一个节点最多有多少个孩子节点,一般用字母m表示阶数。
我们再举个例子来说明一下上面的概念,比如这里有一个5阶的B树,根节点数量范围:1 <= k <= 4,非根节点数量范围:2 <= k <= 4。
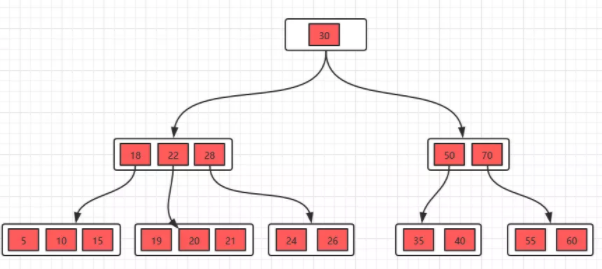
B+树
B+树其实和B树是非常相似的,我们首先看看相同点。
- 根节点至少一个元素
- 非根节点元素范围:m/2 <= k <= m-1
不同点:
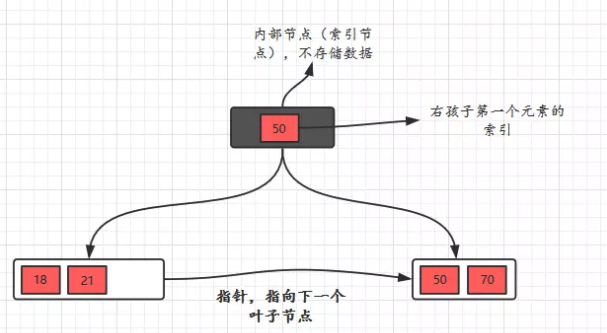
- B+树有两种类型的节点:内部结点(也称索引结点)和叶子结点。内部节点就是非叶子节点,内部节点不存储数据,只存储索引,数据都存储在叶子节点。
- 内部结点中的key都按照从小到大的顺序排列,对于内部结点中的一个key,左树中的所有key都小于它,右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
- 每个叶子结点都存有相邻叶子结点的指针,叶子结点本身依关键字的大小自小而大顺序链接。
- 父节点存有右孩子的第一个元素的索引。
B树(B-树)和B+树区别
- 关键字数量不同:B+树分支结点M个关键字,叶子节点也有M个;B树分支结点则存在 k-1 个关键码
- 数据存储位置不同:B+树数据存储在叶子结点上;B树存储在每个结点上;
- 查询不同:B+树是从根节点到叶子节点的路径;B树是只需要找到数据就可以
- 分支节点存储信息不同:B+树存索引信息;B树存的是数据关键字
小结
B树/B-树:多路搜索树,每个结点存储M/2到M个关键字,非叶子结点存储指向关键字范围的子结点;所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中;
B+树:在B-树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中;
B+树相对于B树有一些自己的优势,可以归结为下面几点。
- 单一节点存储的元素更多,使得查询的IO次数更少,所以也就使得它更适合做为数据库MySQL的底层数据结构了。
- 所有的查询都要查找到叶子节点,查询性能是稳定的,而B树,每个节点都可以查找到数据,所以不稳定。
- 所有的叶子节点形成了一个有序链表,更加便于查找。
二叉树的遍历与实现
递归实现二叉树的遍历
前序遍历

基本思想:若二叉树为空,则返回。否则从根结点开始,优先访问根结点,再前序遍历左子树,前序遍历右子树,即根——左——右
图中按照前序遍历的访问结果为:A、B、D、G、H、C、E、I、F
/**
* 前序遍历(根左右)
* output:A、B、D、G、H、C、E、I、F
* @param root
*/
public void preOrder(TreeNode root) {
if (root == null) {
return;
} else {
System.out.println("preOrder data:" + root.getData());
preOrder(root.leftChild);
preOrder(root.rightChild);
}
}
中序遍历
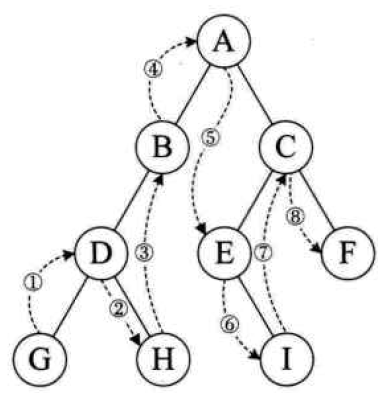
基本思想:若二叉树为空,则返回。否则优先中序遍历左子树,再访问根结点,再后序遍历右子树,即左——根——右
图中按照中序遍历的访问结果为:G、D、H、B、A、E、I、C、F
使用代码递归来实现中序遍历,如下所示:
/**
* 中序遍历(左根右)
* output:G、D、H、B、A、E、I、C、F
* @param root
*/
public void midOrder(TreeNode root) {
if (root == null) {
return;
} else {
midOrder(root.leftChild);
System.out.println("midOrder data:" + root.getData());
midOrder(root.rightChild);
}
}
后序遍历
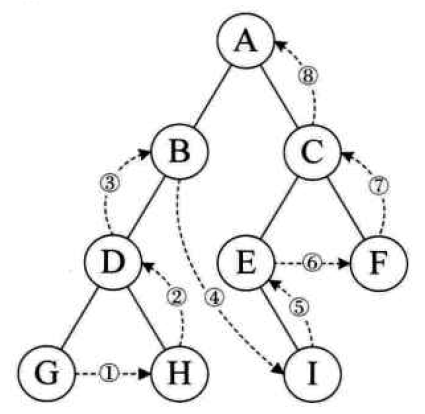
基本思想:若二叉树为空,则返回。否则优先后序遍历左子树,再后序遍历右子树,最后访问根结点,,即左——右——根
图中按照后序遍历的访问结果为:G、H、D、B、I、E、F、C、A
使用代码递归来实现后序遍历,如下所示:
/**
* 后序遍历(左右根)
* output:G、H、D、B、I、E、F、C、A
* @param root
*/
public void postOrder(TreeNode root){
if (root == null) {
return;
} else {
postOrder(root.leftChild);
postOrder(root.rightChild);
System.out.println("postOrder data:" + root.getData());
}
}
非递归实现二叉树的遍历
利用栈进行前序遍历
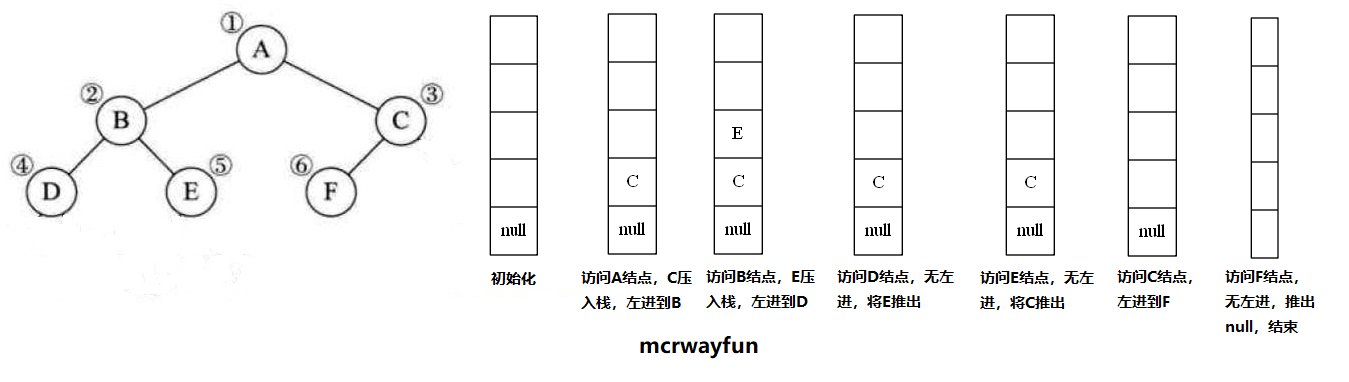
每访问一个结点后,在向左子树遍历下去之前,利用栈来记录该结点的右子女(如果有的话),以便在左子树退回时可以直接从栈顶取得右子树的根结点,继续其右子树的遍历。上图是过程的演示,先将null压入栈中,当栈中无元素时将其推出,表示结束。
/**
* 前序遍历非递归算法
* output:A-B-D-E-C-F
* @param root
*/
public void preOrderNonRecursive(TreeNode root) {
Stack<TreeNode> nodeStack = new Stack<>();
nodeStack.push(null);
while (root != null) {
// 访问根结点
System.out.println("preOrderNonRecursive data:" + root.getData());
// 当前结点右子树不为空则放入栈中
if (root.rightChild != null)
nodeStack.push(root.rightChild);
// 访问左子树
if (root.leftChild != null)
root = root.leftChild;
else root = nodeStack.pop();
}
}
利用栈进行中序遍历
从根结点开始沿着leftChild到最下角的结点,将指针依次压入栈中,直到该结点的leftChild指针为NULL。访问它的数据后,再遍历该结点的右子树。此时该结点为栈中推出的指针。
/**
* 中序遍历非递归算法
* output:D-B-E-A-F-C
* @param root
*/
public void midOrderNonRecursive(TreeNode root) {
Stack<TreeNode> nodeStack = new Stack<>();
do {
while (root != null) {
nodeStack.push(root);
root = root.leftChild;
}
if (!nodeStack.empty()) {
root = nodeStack.pop();
System.out.println("preOrderNonRecursive data:" + root.getData());
root = root.rightChild;
}
} while (root != null || !nodeStack.empty());
}
利用栈进行后序遍历
因为后序遍历的访问顺序为左右根,所以在访问的时候比较麻烦,需要考虑到访问完左结点后,当前结点有无右结点需要访问,若有则需要右进访问右子树,所以要有一个变量来记录当前结点。
- 从根结点开始沿着leftChild到最下角的结点,将指针依次压入栈中,直到该结点的leftChild指针为NULL。
- 判断当前结点有无右子树,若有,则优先访问右子树
- 无右子树货已经访问过右子树则访问当前结点
/**
* 后序遍历非递归算法
* output:D-E-B-F-C-A
*
* @param root
*/
public void postOrderNonRecursive(TreeNode root) {
Stack<TreeNode> nodeStack = new Stack<>();
// 上一个结点
TreeNode prev = root;
do {
while (root != null) {
nodeStack.push(root);
root = root.leftChild;
}
// 访问当前结点的右结点
if (!nodeStack.empty()) {
// 获取右子树,但先不弹出
TreeNode temp = nodeStack.peek().rightChild;
// 不存在右子树或右子树已经访问过,可以访问父结点
if (temp == null || temp == prev) {
root = nodeStack.pop();
System.out.println("postOrderNonRecursive data:" + root.getData());
// 记录访问过的结点
prev = root;
// 当前结点置空
root = null;
} else {
// 存在右子树,需要优先访问右子树
root = temp;
}
}
} while (root != null || !nodeStack.empty());
}
获取二叉树的高度和度
获取二叉树高度
树的性质第12点:叶结点的高度为1,非叶结点的高度等于它子女结点高度的最大值加1。核心思想是递归实现
/**
* 求二叉树的深度(高度)
*
* @return
*/
public int getHeight() {
return getHeight(root);
}
/**
* 求二叉树的深度(高度)
*
* @param root
* @return
*/
private int getHeight(TreeNode root) {
if (root == null) {
return 0;
} else {
int i = getHeight(root.leftChild);
int j = getHeight(root.rightChild);
return i >= j ? i + 1 : j + 1;
}
}
获取二叉树的度
/**
* 求二叉树的结点数
*
* @return
*/
public int getSize() {
return getSize(root);
}
/**
* 求二叉树的结点数
*
* @param root
* @return
*/
private int getSize(TreeNode root) {
if (root == null) {
return 0;
} else {
return 1 + getSize(root.leftChild) + getSize(root.rightChild);
}
}
创建一棵二叉树
// 结点类
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public class CreateBinaryTree {
// 前序遍历测试
public static void main(String[] args) {
TreeNode node = CreateBinaryTree.createBT(new int[]{1, 2, 3, 4, 5,6}, 0);
CreateBinaryTree.preOrder(node); //124536
}
// 构建二叉树 (完全二叉树)
public static TreeNode createBT(int[] arr, int i) // 初始时,传入的i==0
{
TreeNode root = null; // 定义根节点
if (i >= arr.length) // i >= arr.length 时,表示已经到达了根节点
return null;
root = new TreeNode(arr[i]); // 根节点
root.left = createBT(arr, 2 * i + 1); // 递归建立左孩子结点
root.right = createBT(arr, 2 * i + 2); // 递归建立右孩子结点
return root;
}
/**
* @description: 前序遍历
*/
public static void preOrder(TreeNode root) {
if (root == null) {
return;
} else {
System.out.println("preOrder data:" + root.val);
preOrder(root.left);
preOrder(root.right);
}
}
}
层序遍历
层序遍历依照从根结点开始,自上而下,从左到右。需要有一个结构来存储当前层的结点,当访问完当前层结点后,将其抛出后继续访问下层结点,队列的先进先出符合这一要求。
- 将根结点压入队列中
- 队列不为空则开始循环,此时只有根结点,则推出根结点并访问。判断根结点有无左右子树,若有则将其压入队列中
- 队列为空,结束循环
/**
* 层序遍历
*
* @param root
*/
public List<List<String>> levelOrder(TreeNode root) {
List<List<String>> reList = new ArrayList<>();
Queue<TreeNode> nodeQueue = new LinkedList<>();
// 压入根结点
nodeQueue.offer(root);
while (!nodeQueue.isEmpty()) {
int levelSize = nodeQueue.size();
List<String> subList = new ArrayList<>();
while (levelSize != 0) {
TreeNode temp = nodeQueue.poll();
subList.add(temp.getData() + "");
if (temp.leftChild != null) nodeQueue.offer(temp.leftChild);
if (temp.rightChild != null) nodeQueue.offer(temp.rightChild);
levelSize--;
}
reList.add(subList);
}
return reList;
}
通过前序遍历复制一棵二叉树
为了实现二叉树的复制方法,可以利用二叉树的前序遍历算法。若二叉树parent不为空,则首先复制根结点,这相当于二叉树前序遍历中访问根结点的语句;然后分别复制二叉树的左子树和右子树,这相当于二叉树前序遍历算法中的遍历左子树和右子树。整个算法的思想是递归。
/**
* 复制一棵二叉树
* @param parent
* @return
*/
public TreeNode copy(TreeNode parent){
if(parent == null)
return null;
// 构造根结点
TreeNode temp = new TreeNode(parent.getIndex(),parent.getData());
// 递归构造左子树
temp.leftChild = copy(parent.leftChild);
// 递归构造右子树
temp.rightChild = copy(parent.rightChild);
return temp;
}
判断两棵树是否相等
递归判断每个结点的s.data == t.data是否成立即可
/**
* 判断两棵树是否相等
* @param s
* @param t
* @return
*/
public boolean euqal(TreeNode s,TreeNode t){
if(s == null && t == null)
return true;
if(s != null && t != null && s.data == t.data &&
euqal(s.leftChild,t.leftChild) &&
euqal(s.rightChild,t.rightChild))
return true;
else
return false;
}
既已览卷至此,何不品评一二: