LeetSilinceCode
算法思想
双指针
| 题目 | 算法思想 |
|---|---|
| #11 盛最多水的容器 | 双指针 |
| #167 有序数组的 Two Sum | 双指针/二分查找 |
| #633 两数平方和 | 双指针 |
| #345 反转字符串中的元音字符 | 双指针 |
| #680 回文字符串 | 双指针 |
| #88 合并两个有序数组 | 双指针 |
| #141 判断链表是否存在环 ⭐️ | 快慢指针 |
| #524 最长子序列 | 双指针 |
| #5. 最长回文子串 | 双指针-中间开始向两边扩散 |
滑动窗口
| 题目 | 算法思想 |
|---|---|
| #3 无重复字符的最长子串 | 滑动窗口 |
| #76 最小覆盖子串 | 滑动窗口 |
| #438 找到字符串中所有字母异位词 | 滑动窗口 |
| #567 字符串的排列 | 滑动窗口 |
滑动窗口算法的思路非常简单,就是维护一个窗口,不断滑动,然后更新答案么。LeetCode 上有起码 10 道运用滑动窗口算法的题目,难度都是中等和困难。该算法的大致逻辑如下:
int left = 0, right = 0;
while (right < s.length()) {
// 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
}
}
这个算法技巧的时间复杂度是 O(N),比字符串暴力算法要高效得多。
其实困扰大家的,不是算法的思路,而是各种细节问题。比如说如何向窗口中添加新元素,如何缩小窗口,在窗口滑动的哪个阶段更新结果。即便你明白了这些细节,也容易出 bug,找 bug 还不知道怎么找,真的挺让人心烦的。
所以今天我就写一套滑动窗口算法的代码框架,我连再哪里做输出 debug 都给你写好了,以后遇到相关的问题,你就默写出来如下框架然后改三个地方就行,还不会出 bug,只需要思考以下四个问题:
1、当移动 right 扩大窗口,即加入字符时,应该更新哪些数据?
2、什么条件下,窗口应该暂停扩大,开始移动 left 缩小窗口?
3、当移动 left 缩小窗口,即移出字符时,应该更新哪些数据?
4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新?
/* 滑动窗口算法框架 */
public String slidingWindow(String s, String t) {
// 需要的字符散列表 全部初始化为1(表示需要)
char[] sArray = s.toCharArray();
HashMap<Character, Integer> need = new HashMap<>();
for (char key : sArray) {
need.put(key, need.getOrDefault(key, 0) + 1);
}
HashMap<Character, Integer> window = new HashMap<>();// 用于记录「窗口」中的相应字符的出现次数
int left = 0, right = 0;
int valid = 0; // 表示窗口中满足need条件的字符个数
while (right < sArray.length) {
// in 是将移入窗口的字符
char in = sArray[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
System.out.println("window: [" + left + "," + right + "]\n");
/********************/
// 判断左侧窗口是否要收缩
while (valid==need.size()) {
// out 是将移出窗口的字符
char out = sArray[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
其中两处 ... 表示的更新窗口数据的地方,到时候你直接往里面填就行了。
而且,这两个 ... 处的操作分别是右移和左移窗口更新操作,等会你会发现它们操作是完全对称的。
说句题外话,我发现很多人喜欢执着于表象,不喜欢探求问题的本质。比如说有很多人评论我这个框架,说什么散列表速度慢,不如用数组代替散列表;还有很多人喜欢把代码写得特别短小,说我这样代码太多余,影响编译速度,LeetCode 上速度不够快。
我服了。算法看的是时间复杂度,你能确保自己的时间复杂度最优,就行了。至于 LeetCode 所谓的运行速度,那个都是玄学,只要不是慢的离谱就没啥问题,根本不值得你从编译层面优化,不要舍本逐末……
言归正传,下面就直接上四道 LeetCode 原题来套这个框架,其中第一道题第一道题会详细说明其原理,后面四道就直接闭眼睛秒杀了。
排序算法
| 题目 | 算法思想 |
|---|---|
| #215 数组中的第K个最大元素/topK ⭐️ | 快速排序/堆排序 |
| #347 前 K 个高频元素 | 桶排序 |
| #451 根据字符出现频率排序 | 桶排序 |
| #75 颜色分类 | |
| #剑指 Offer 45 把数组排成最小的数 ⭐️ | 自定义排序 |
// 快速排序
Random random = new Random();
public static void quickSort(int[] nums, int start, int end) {
if(start>=end) return; // 只有一个元素时终止
int left = start;
int right = end;
// 随机选择枢纽点
int i =random.nextInt(end - start + 1)+start;
int temp = nums[left];
nums[left]=nums[i];
nums[i]=temp;
int pivot = nums[left]; // 枢纽点pivot选取第一个元素
while (left < right) {
// high指针往左寻找一个小于 pivot的数
while (left<right&&nums[right]>=pivot) {
right--;
}
nums[left]=nums[right]; // 将小于 pivot 的数放在低位
// low指针往右寻找一个大于 pivot 的数
while (left<right&&nums[left]<=pivot) {
left++;
}
nums[right]=nums[left]; // 将大于 pivot 的数放在高位
}
// 复原 pivot的值
nums[left] = pivot;
quickSort(nums, start, left - 1); // 递归排序左半部分
quickSort(nums, left + 1, end); // 递归排序右半部分
}
堆排序
- 堆排序就是利用大顶堆或者小顶堆的特性来进行排序的。它的基本思想就是:
- 给定以下一个数组,(完全二叉树一般用数组来存储)。
- 初始化大顶堆,我们需要从树的最后一层开始,逐渐的把大值向上调整(左右孩子节点中较大的节点和父节点交换),直到第一层。
- 取出排序。既然构建成堆结构了,那么接下来,我们取出堆顶的数据,也就是数组第一个数 9 ,取法是将数组的第一位和最后一位调换,然后将数组的待排序的范围 -1。
- 初始化堆 O(m); 每次取出堆顶元素时候需调整为大顶堆的时间复杂度为 O(logm)。因此堆排序的复杂度为1次建堆和n次调整的复杂度O(m+nlogm)=O(nlogm)。
// 堆排序
public static void sort(int[] arr) {
int length = arr.length;
//构建堆
buildHeap(arr, length);
for ( int i = length - 1; i > 0; i-- ) {
//将堆顶元素与末位元素调换
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
//数组长度-1 隐藏堆尾元素
length--;
//将堆顶元素下沉 目的是将最大的元素浮到堆顶来
sink(arr, 0, length);
}
}
private static void buildHeap(int[] arr, int length) {
for (int i = length / 2; i >= 0; i--) {
sink(arr, i, length);
}
}
/**
* 下沉调整
* @param arr 数组
* @param index 调整位置
* @param length 数组范围
*/
private static void sink(int[] arr, int index, int length) {
int leftChild = 2 * index + 1;//左子节点下标
int rightChild = 2 * index + 2;//右子节点下标
int present = index;//要调整的节点下标
//下沉左边
if (leftChild < length && arr[leftChild] > arr[present]) {
present = leftChild;
}
//下沉右边
if (rightChild < length && arr[rightChild] > arr[present]) {
present = rightChild;
}
//如果下标不相等 证明调换过了
if (present != index) {
//交换值
int temp = arr[index];
arr[index] = arr[present];
arr[present] = temp;
//继续下沉
sink(arr, present, length);
}
}
贪心思想
| 题目 | 算法思想 |
|---|---|
| #435. 无重叠区间(中等) | 贪心算法 |
| #452.用最少数量的箭引爆气球(中等) | 贪心算法 |
什么是贪心算法呢?贪心算法可以认为是动态规划算法的一个特例,相比动态规划,使用贪心算法需要满足更多的条件(贪心选择性质),但是效率比动态规划要高。
比如说一个算法问题使用暴力解法需要指数级时间,如果能使用动态规划消除重叠子问题,就可以降到多项式级别的时间,如果满足贪心选择性质,那么可以进一步降低时间复杂度,达到线性级别的。
什么是贪心选择性质呢,简单说就是:每一步都做出一个局部最优的选择,最终的结果就是全局最优。注意哦,这是一种特殊性质,其实只有一部分问题拥有这个性质。
比如你面前放着 100 张人民币,你只能拿十张,怎么才能拿最多的面额?显然每次选择剩下钞票中面值最大的一张,最后你的选择一定是最优的。
然而,大部分问题明显不具有贪心选择性质。比如打斗地主,对手出对儿三,按照贪心策略,你应该出尽可能小的牌刚好压制住对方,但现实情况我们甚至可能会出王炸。这种情况就不能用贪心算法,而得使用动态规划解决,参见前文「动态规划解决博弈问题」。
言归正传,本文解决一个很经典的贪心算法问题 Interval Scheduling(区间调度问题)。给你很多形如 [start, end] 的闭区间,请你设计一个算法,算出这些区间中最多有几个互不相交的区间。
int intervalSchedule(int[][] intvs) {}
举个例子,intvs = [[1,3], [2,4], [3,6]],这些区间最多有 2 个区间互不相交,即 [[1,3], [3,6]],你的算法应该返回 2。注意边界相同并不算相交。
这个问题在生活中的应用广泛,比如你今天有好几个活动,每个活动都可以用区间 [start, end] 表示开始和结束的时间,请问你今天最多能参加几个活动呢?显然你一个人不能同时参加两个活动,所以说这个问题就是求这些时间区间的最大不相交子集。
正确的思路其实很简单,可以分为以下三步:
- 从区间集合 intvs 中选择一个区间 x,这个 x 是在当前所有区间中结束最早的(end 最小)。
- 把所有与 x 区间相交的区间从区间集合 intvs 中删除。
- 重复步骤 1 和 2,直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。
把这个思路实现成算法的话,可以按每个区间的 end 数值升序排序,因为这样处理之后实现步骤 1 和步骤 2 都方便很多:
public int getResult(int[][] intvs){
Arrays.sort(intvs,(a,b)->a[1]-b[1]);
int count = 1;
int xEnd = intvs[0][1];
for (int[] intv : intvs) {
int start = intv[0];
if (start>=xEnd){
count++;
xEnd = intv[1];
}
}
return count;
}
二分查找
| 题目 | 算法思想 |
|---|---|
| #704 二分查找 | 二分查找 |
| #34 在排序数组中查找元素的第一个和最后一个位置 | 二分查找 |
| 判定子序列 | 二分查找 |
| 分段和最大值最小 | 二分check |
二分查找并不简单,Knuth 大佬(发明 KMP 算法的那位)都说二分查找:思路很简单,细节是魔鬼。很多人喜欢拿整型溢出的 bug 说事儿,但是二分查找真正的坑根本就不是那个细节问题,而是在于到底要给 mid 加一还是减一,while 里到底用 <= 还是 <。
你要是没有正确理解这些细节,写二分肯定就是玄学编程,有没有 bug 只能靠菩萨保佑。我特意写了一首诗来歌颂该算法,概括本文的主要内容,建议保存:

本文就来探究几个最常用的二分查找场景:寻找一个数、寻找左侧边界、寻找右侧边界。而且,我们就是要深入细节,比如不等号是否应该带等号,mid 是否应该加一等等。分析这些细节的差异以及出现这些差异的原因,保证你能灵活准确地写出正确的二分查找算法。
0.二分查找框架:
int binarySearch(int[] nums, int target) {
int left = 0, right = ...;
while(...) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
...
} else if (nums[mid] < target) {
left = ...
} else if (nums[mid] > target) {
right = ...
}
}
return ...;
}
分析二分查找的一个技巧是:不要出现 else,而是把所有情况用 else if 写清楚,这样可以清楚地展现所有细节。本文都会使用 else if,旨在讲清楚,读者理解后可自行简化。
其中 ... 标记的部分,就是可能出现细节问题的地方,当你见到一个二分查找的代码时,首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。
另外声明一下,计算 mid 时需要防止溢出,代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同,但是有效防止了 left 和 right 太大直接相加导致溢出。
1.寻找一个数(基本的二分搜索)
这个场景是最简单的,可能也是大家最熟悉的,即搜索一个数,如果存在,返回其索引,否则返回 -1。
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
1)为什么 while 循环的条件中是 <=,而不是 <?
答:因为初始化 right 的赋值是 nums.length - 1,即最后一个元素的索引,而不是 nums.length。
这二者可能出现在不同功能的二分查找中,区别是:前者相当于两端都闭区间 [left, right],后者相当于左闭右开区间 [left, right),因为索引大小为 nums.length 是越界的。
我们这个算法中使用的是前者 [left, right] 两端都闭的区间。这个区间其实就是每次进行搜索的区间。
什么时候应该停止搜索呢?当然,找到了目标值的时候可以终止:
if(nums[mid] == target)
return mid;
但如果没找到,就需要 while 循环终止,然后返回 -1。那 while 循环什么时候应该终止?搜索区间为空的时候应该终止,意味着你没得找了,就等于没找到嘛。
while(left <= right) 的终止条件是 left == right + 1,写成区间的形式就是 [right + 1, right],或者带个具体的数字进去 [3, 2],可见这时候区间为空,因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的,直接返回 -1 即可。
while(left < right) 的终止条件是 left == right,写成区间的形式就是 [right, right],或者带个具体的数字进去 [2, 2],这时候区间非空,还有一个数 2,但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了,索引 2 没有被搜索,如果这时候直接返回 -1 就是错误的。
当然,如果你非要用 while(left < right) 也可以,我们已经知道了出错的原因,就打个补丁好了:
//...
while(left < right) {
// ...
}
return nums[left] == target ? left : -1;
2)为什么 ,right = mid - 1?我看有的代码是 right = mid 或者 left = mid,没有这些加加减减,到底怎么回事,怎么判断?
答:这也是二分查找的一个难点,不过只要你能理解前面的内容,就能够很容易判断。
刚才明确了「搜索区间」这个概念,而且本算法的搜索区间是两端都闭的,即 [left, right]。那么当我们发现索引 mid 不是要找的 target 时,下一步应该去搜索哪里呢?
当然是去搜索 [left, mid-1] 或者 [mid+1, right] 对不对?因为 mid 已经搜索过,应该从搜索区间中去除。
3)此算法有什么缺陷?
答:至此,你应该已经掌握了该算法的所有细节,以及这样处理的原因。但是,这个算法存在局限性。
比如说给你有序数组 nums = [1,2,2,2,3],target 为 2,此算法返回的索引是 2,没错。但是如果我想得到 target 的左侧边界,即索引 1,或者我想得到 target 的右侧边界,即索引 3,这样的话此算法是无法处理的。
这样的需求很常见,你也许会说,找到一个 target,然后向左或向右线性搜索不行吗?可以,但是不好,因为这样难以保证二分查找对数级的复杂度了。
我们后续的算法就来讨论这两种二分查找的算法。
2.寻找左侧边界的二分搜索
以下是最常见的代码形式,其中的标记是需要注意的细节:
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0;
int right = nums.length; // 注意
while (left < right) { // 注意
int mid = (left + right) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid; // 为什么不需要减1 因为搜索区间是[low,high)
}
}
return left;
}
1)为什么 while 中是 < 而不是 <=?
答:用相同的方法分析,因为 right = nums.length 而不是 nums.length - 1。因此每次循环的「搜索区间」是 [left, right) 左闭右开。
while(left < right) 终止的条件是 left == right,此时搜索区间 [left, left) 为空,所以可以正确终止。
PS:这里先要说一个搜索左右边界和上面这个算法的一个区别,也是很多读者问的:刚才的 right 不是 nums.length - 1 吗,为啥这里非要写成 nums.length 使得「搜索区间」变成左闭右开呢?
因为对于搜索左右侧边界的二分查找,这种写法比较普遍,我就拿这种写法举例了,保证你以后遇到这类代码可以理解。你非要用两端都闭的写法反而更简单,我会在后面写相关的代码,把三种二分搜索都用一种两端都闭的写法统一起来,你耐心往后看就行了。
⭐️ 2)为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办?
答:因为要一步一步来,先理解一下这个「左侧边界」有什么特殊含义:
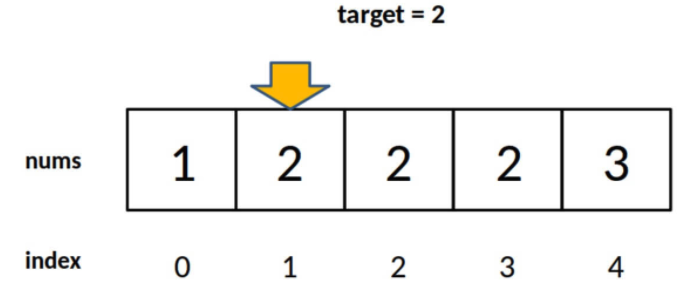
对于这个数组,算法会返回 1。这个 1 的含义可以这样解读:nums 中小于 2 的元素有 1 个。
比如对于有序数组 nums = [2,3,5,7], target = 1,算法会返回 0,含义是:nums 中小于 1 的元素有 0 个。
再比如说 nums = [2,3,5,7], target = 8,算法会返回 4,含义是:nums 中小于 8 的元素有 4 个。
综上可以看出,函数的返回值(即 left 变量的值)取值区间是闭区间 [0, nums.length],所以我们简单添加两行代码就能在正确的时候 return -1:
while (left < right) {
//...
}
// target 比所有数都大
if (left == nums.length) return -1;
// 类似之前算法的处理方式
if (nums[left] != target) return -1;
3)为什么 left = mid + 1,right = mid ?和之前的算法不一样?
答:这个很好解释,因为我们的「搜索区间」是 [left, right) 左闭右开,所以当 nums[mid] 被检测之后,下一步的搜索区间应该去掉 mid 分割成两个区间,即 [left, mid) 或 [mid + 1, right)。
4)为什么该算法能够搜索左侧边界?
答:关键在于对于 nums[mid] == target 这种情况的处理:
if (nums[mid] == target)
right = mid;
可见,找到 target 时不要立即返回,而是缩小「搜索区间」的上界 right,在区间 [left, mid) 中继续搜索,即不断向左收缩,达到锁定左侧边界的目的。
5)为什么返回 left 而不是 right?
答:都是一样的,因为 while 终止的条件是 left == right。
6)能不能想办法把 right 变成 ,也就是继续使用两边都闭的「搜索区间」?这样就可以和第一种二分搜索在某种程度上统一起来了。
答:当然可以,只要你明白了「搜索区间」这个概念,就能有效避免漏掉元素,随便你怎么改都行。下面我们严格根据逻辑来修改:
因为你非要让搜索区间两端都闭,所以 right 应该初始化为 nums.length - 1,while 的终止条件应该是 left == right + 1,也就是其中应该用 <=:
int left_bound(int[] nums, int target) {
// 搜索区间为 [left, right]
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
// if else ...
}
因为搜索区间是两端都闭的,且现在是搜索左侧边界,所以 left 和 right 的更新逻辑如下:
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
由于 while 的退出条件是 left == right + 1,所以当 target 比 nums 中所有元素都大时,会存在以下情况使得索引越界:
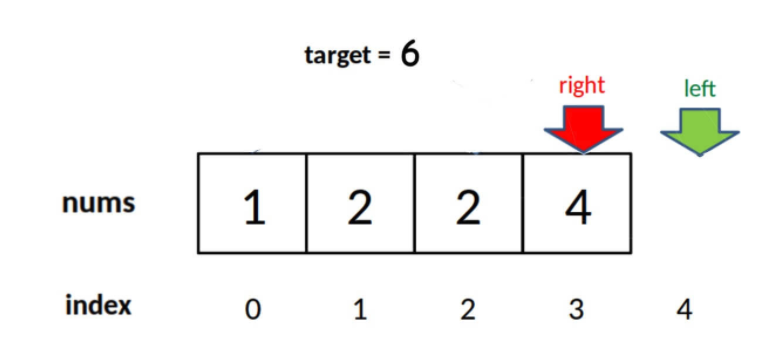
因此,最后返回结果的代码应该检查越界情况:
if (left >= nums.length || nums[left] != target)
return -1;
return left;
至此,整个算法就写完了,完整代码如下:
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// 搜索区间为 [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
}
// 检查出界情况
if (left >= nums.length || nums[left] != target)
return -1;
return left;
}
这样就和第一种二分搜索算法统一了,都是两端都闭的「搜索区间」,而且最后返回的也是 left 变量的值。只要把住二分搜索的逻辑,两种形式大家看自己喜欢哪种记哪种吧。
3.寻找右侧边界的二分查找
类似寻找左侧边界的算法,这里也会提供两种写法,还是先写常见的左闭右开的写法,只有两处和搜索左侧边界不同,已标注:
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = (left + right) / 2;
if (nums[mid] == target) {
left = mid + 1; // 注意
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1; // 注意
}
1)为什么这个算法能够找到右侧边界?
答:类似地,关键点还是这里:
if (nums[mid] == target) {
left = mid + 1;
当 nums[mid] == target 时,不要立即返回,而是增大「搜索区间」的下界 left,使得区间不断向右收缩,达到锁定右侧边界的目的。
2)为什么最后返回 left - 1 而不像左侧边界的函数,返回 left?而且我觉得这里既然是搜索右侧边界,应该返回 right 才对。
答:首先,while 循环的终止条件是 left == right,所以 left 和 right 是一样的,你非要体现右侧的特点,返回 right - 1 好了。
至于为什么要减一,这是搜索右侧边界的一个特殊点,关键在这个条件判断:
if (nums[mid] == target) {
left = mid + 1;
// 这样想: mid = left - 1
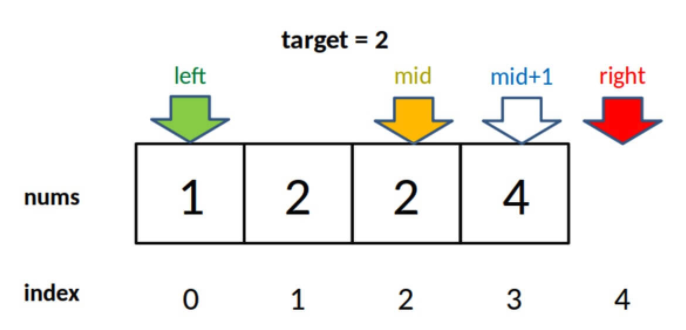
因为我们对 left 的更新必须是 left = mid + 1,就是说 while 循环结束时,nums[left] 一定不等于 target 了,而 nums[left-1] 可能是 target。
至于为什么 left 的更新必须是 left = mid + 1,同左侧边界搜索,就不再赘述。
3)为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办?
答:类似之前的左侧边界搜索,因为 while 的终止条件是 left == right,就是说 left 的取值范围是 [0, nums.length],所以可以添加两行代码,正确地返回 -1:
while (left < right) {
// ...
}
if (left == 0) return -1;
return nums[left-1] == target ? (left-1) : -1;
4)是否也可以把这个算法的「搜索区间」也统一成两端都闭的形式呢?这样这三个写法就完全统一了,以后就可以闭着眼睛写出来了。
答:当然可以,类似搜索左侧边界的统一写法,其实只要改两个地方就行了:
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 这里改成收缩左侧边界即可
left = mid + 1;
}
}
// 这里改为检查 right 越界的情况,见下图
if (right < 0 || nums[right] != target)
return -1;
return right;
}
当 target 比所有元素都小时,right 会被减到 -1,所以需要在最后防止越界:
至此,搜索右侧边界的二分查找的两种写法也完成了,其实将「搜索区间」统一成两端都闭反而更容易记忆,你说是吧?
4.逻辑统一
来梳理一下这些细节差异的因果逻辑:
第一个,最基本的二分查找算法:
因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1
因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回
第二个,寻找左侧边界的二分查找:
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界
第三个,寻找右侧边界的二分查找:
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界
又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right,必须减一
对于寻找左右边界的二分搜索,常见的手法是使用左闭右开的「搜索区间」,我们还根据逻辑将「搜索区间」全都统一成了两端都闭,便于记忆,只要修改两处即可变化出三种写法:
int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
// 最后要检查 left 越界的情况
if (left >= nums.length || nums[left] != target)
return -1;
return left;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
// 最后要检查 right 越界的情况
if (right < 0 || nums[right] != target)
return -1;
return right;
}
如果以上内容你都能理解,那么恭喜你,二分查找算法的细节不过如此。
动态规划
| 题目 | 算法思想 |
|---|---|
| #509 斐波那契数 | 动态规划 |
| #322 零钱兑换 | 动态规划 |
| #72. 编辑距离 | 子序列问题/动态规划 |
| #152.乘积最大子数组 | 动态规划 |
| #300. 最长递增子序列 | 子序列问题/动态规划 |
| 乘积最大⭐️ | 动态规划 |
| #354. 俄罗斯套娃信封问题 | 子序列问题/动态规划 |
| #53. 最大子序和 | 子序列问题/最大子数组/动态规划 |
| #1143. 最长公共子序列 | 最长公共子序列问题/动态规划 |
| #583. 两个字符串的删除操作 | 最长公共子序列问题/动态规划 |
| #712. 两个字符串的最小ASCII删除和 | 最长公共子序列问题/动态规划 |
| #516. 最长回文子序列 | 动态规划 |
| #91. 解码方法 | 动态规划 |
首先,动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法,只不过在计算机问题上应用比较多,比如说让你求最长递增子序列呀,最小编辑距离呀等等。
既然是要求最值,核心问题是什么呢?求解动态规划的核心问题是穷举。因为要求最值,肯定要把所有可行的答案穷举出来,然后在其中找最值呗。
动态规划这么简单,就是穷举就完事了?我看到的动态规划问题都很难啊!
首先,动态规划的穷举有点特别,因为这类问题存在「重叠子问题」,如果暴力穷举的话效率会极其低下,所以需要「备忘录」或者「DP table」来优化穷举过程,避免不必要的计算。
而且,动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。
另外,虽然动态规划的核心思想就是穷举求最值,但是问题可以千变万化,穷举所有可行解其实并不是一件容易的事,只有列出正确的「状态转移方程」才能正确地穷举。
以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解,但是在实际的算法问题中,写出状态转移方程是最困难的,这也就是为什么很多朋友觉得动态规划问题困难的原因,我来提供我研究出来的一个思维框架,辅助你思考状态转移方程:
定义 dp 数组/函数的含义 -> 明确 base case -> 明确「状态」-> 明确「选择」。
按上面的套路走,最后的结果就可以套这个框架:
# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 求最值(选择1,选择2...)
第一个斐波那契数列的问题,解释了如何通过「备忘录」或者「dp table」的方法来优化递归树,并且明确了这两种方法本质上是一样的,只是自顶向下和自底向上的不同而已。
第二个凑零钱的问题,展示了如何流程化确定「状态转移方程」,只要通过状态转移方程写出暴力递归解,剩下的也就是优化递归树,消除重叠子问题而已。
计算机解决问题其实没有任何奇技淫巧,它唯一的解决办法就是穷举,穷举所有可能性。算法设计无非就是先思考“如何穷举”,然后再追求“如何聪明地穷举”。
列出动态转移方程,就是在解决“如何穷举”的问题。之所以说它难,一是因为很多穷举需要递归实现,二是因为有的问题本身的解空间复杂,不那么容易穷举完整。
备忘录、DP table 就是在追求“如何聪明地穷举”。用空间换时间的思路。
背包问题
| 题目 | 算法思想 |
|---|---|
| #322. 零钱兑换 | 完全背包最值问题:外循环coins,内循环amount正序 |
| #494. 目标和 | 0-1背包不考虑元素顺序的组合问题:选nums里的数得到target的种数,外循环nums,内循环target倒序 |
| #416. 分割等和子集 | 0-1背包存在性问题:是否存在一个子集,其和为target=sum/2,外循环nums,内循环target倒序 |
| #518. 零钱兑换 II | 完全背包不考虑顺序的组合问题:外循环coins,内循环target正序 |
| 279. 完全平方数 | 完全背包的最值问题:外循环nums,内循环target正序 |
| 377. 组合总和 Ⅳ | 考虑顺序的组合问题:外循环target,内循环nums |
| 1049. 最后一块石头的重量 II | 0/1背包最值问题:外循环stones,内循环target=sum/2倒序 |
回溯算法
| 题目 | 算法思想 |
|---|---|
| #46. 全排列 | 回溯算法 |
| 剑指 Offer 38 字符串的排列 ⭐️ | 回溯算法 |
| #51. N 皇后 | 回溯算法 |
| #494. 目标和 | 动态规划/背包问题 |
| #22. 括号生成 ⭐️ | 回溯算法 |
| #131. 分割回文串 | 回溯算法+动态规划 |
解决一个回溯问题,实际上就是一个决策树的遍历过程。你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
代码方面,回溯算法的框架:
- 写
backtrack函数时,需要维护走过的「路径」和当前可以做的「选择列表」,当触发「结束条件」时,将「路径」记入结果集。 - 其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,特别简单。
# 回溯模版
List<String> result = new ArrayList<String>();
public void backtrack(路径, 选择列表):
if (满足结束条件): // 递归出口
result.add(路径)
return;
for 选择 in 选择列表:
// 做选择
backtrack(路径, 选择列表)
// 撤销选择
其实想想看,回溯算法和动态规划是不是有点像呢?我们在动态规划系列文章中多次强调,动态规划的三个需要明确的点就是「状态」「选择」和「base case」,是不是就对应着走过的「路径」,当前的「选择列表」和「结束条件」?
某种程度上说,动态规划的暴力求解阶段就是回溯算法。只是有的问题具有重叠子问题性质,可以用 dp table 或者备忘录优化,将递归树大幅剪枝,这就变成了动态规划。而今天的两个问题,都没有重叠子问题,也就是回溯算法问题了,复杂度非常高是不可避免的。
BFS算法
| 题目 | 算法思想 |
|---|---|
| #111. 二叉树的最小深度 | BFS算法 |
| #752. 打开转盘锁 | BFS算法 |
首先,你要说 labuladong 没写过 BFS 框架,这话没错,今天写个框架你背住就完事儿了。但要是说没写过 DFS 框架,那你还真是说错了,其实 DFS 算法就是回溯算法。
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度比 DFS 大很多,至于为什么,我们后面介绍了框架就很容易看出来了。
算法框架:
要说框架的话,我们先举例一下 BFS 出现的常见场景好吧,问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿,把枯燥的本质搞清楚了,再去欣赏各种问题的包装才能胸有成竹嘛。
这个广义的描述可以有各种变体,比如走迷宫,有的格子是围墙不能走,从起点到终点的最短距离是多少?如果这个迷宫带「传送门」可以瞬间传送呢?
再比如说两个单词,要求你通过某些替换,把其中一个变成另一个,每次只能替换一个字符,最少要替换几次?
再比如说连连看游戏,两个方块消除的条件不仅仅是图案相同,还得保证两个方块之间的最短连线不能多于两个拐点。你玩连连看,点击两个坐标,游戏是如何判断它俩的最短连线有几个拐点的?
再比如……
净整些花里胡哨的,这些问题都没啥奇技淫巧,本质上就是一幅「图」,让你从一个起点,走到终点,问最短路径。这就是 BFS 的本质,框架搞清楚了直接默写就好:
队列 q 就不说了,BFS 的核心数据结构;cur.adj() 泛指 cur 相邻的节点,比如说二维数组中,cur 上下左右四面的位置就是相邻节点;visited 的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要 visited。
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
LinkedList<TreeNode> queue = new LinkedList<>(); // 核心数据结构
Set<Node> visited; // 避免走回头路
queue.offer(start); // offer是queue的插入方法,将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (!queue.isEmpty()) {
int size = queue.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < size; i++) {
Node cur = queue.poll(); // poll() 检索并删除此列表的头部(第一个元素)
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj())
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
LRU/LFU
| 题目 | 算法思想 |
|---|---|
| #146. LRU缓存机制 | 最近最久未使用 LRU |
| #460. LFU缓存 | 最近最少使用页面 LFU |
数据结构相关
正确率 > 80% 可移除 👩🏻💻
数组
https://leetcode-cn.com/tag/array/
| 题目 | 算法思想 |
|---|---|
| #26 删除排序数组中的重复项 ⭐️ | 双指针 |
| #88 合并两个有序数组 ⭐️ | 双指针 |
| #287. 寻找重复数 | 二分查找/快慢指针 |
| #349. 两个数组的交集 ⭐️ | 哈希表/排序+双指针 |
| #剑指 Offer 03 数组中重复的数字 ⭐️ | 原地交换 |
| #169 多数元素 | 哈希表/排序/随机化/投票法 |
| #674 最长连续递增序列 | 动态规划 |
| #1051 高度检查器 | 桶排序 |
| #1160 拼写单词 | counter方法/HashMap |
| #300. 最长递增子序列 | 动态规划+二分 |
| #283. 移动零 | |
| #566. 重塑矩阵 | |
| #485. 最大连续 1 的个数 | |
| #240. 搜索二维矩阵 II | |
| #378. 有序矩阵中第 K 小的元素 | |
| #645. 错误的集合 | |
| #667. 优美的排列 II | |
| #697. 数组的度 | |
| #766. 托普利茨矩阵 | |
| #565. 数组嵌套 | |
| #769. 最多能完成排序的块 |
链表
链表的题通常需要注意两点:
- 舍得用变量,千万别想着节省变量,否则容易被逻辑绕晕。
- head 有可能需要改动时,先增加一个 假head,返回的时候直接取 假head.next,这样就不需要为修改 head 增加一大堆逻辑了。
| 题目 | 算法思想 |
|---|---|
| #160. 两链表相交 ⭐️ | 无环/有环 |
| #141 判断链表是否存在环 ⭐️ | 快慢指针 |
| #142. 环形链表 II ⭐️ | 数学+快慢指针 |
| #206. 反转链表 ⭐️ | 迭代/递归 |
| #25. K 个一组翻转链表 ⭐️ | 链表分区 |
| 876. 链表的中间结点 ⭐️ | 快慢指针 |
| 21. 合并两个有序链表 ⭐️ | 指针 |
| #143. 重排链表 ⭐️ | 找中点+反转链表+合并链表 |
| #83.删除排序链表中的重复元素⭐️ | 一次遍历 |
| #19.删除链表的倒数第N个结点 ⭐️ | 快慢指针(快指针先走N步)+pre指针+dummyHead |
| #24.两两交换链表中的节点 | |
| #445. 两数相加 II | |
| #234. 回文链表 | |
| #725. 分隔链表 | |
| #328. 奇偶链表 |
二叉树
| 题目 | 算法思想 |
|---|---|
| #144 非递归实现二叉树的前序遍历 ⭐️ | 前序遍历 |
| #145 非递归实现二叉树的后序遍历 ⭐️ | 后序遍历 = reverse(反转树先序遍历) |
| #94 非递归实现二叉树的中序遍历 ⭐️ | 中序遍历 |
| #104.树的高度 ⭐️ | 递归/广度优先 |
| #111.二叉树的最小深度 ⭐️ | 递归/广度优先 |
| 剑指 Offer 28. 对称的二叉树 ⭐️ | 递归 |
| 剑指 Offer 26. 树的子结构 ⭐️ | 先序遍历 + 包含判断 |
| #110 平衡二叉树 | 递归 |
| #543 两节点的最长路径 ⭐️ | 递归 |
| #226 翻转树 ⭐️ | 前序遍历/递归 |
| #116 填充每个节点的下一个右侧节点指针 ⭐️ | 前序遍历/递归 |
| #114. 二叉树展开为链表 ⭐️ | 后序遍历/递归 |
| #617 归并两棵树 | 递归 |
| #654. 最大二叉树 ⭐️ | 递归 |
| #105. 从前序与中序遍历序列构造二叉树 ⭐️ | 递归 |
| #106. 从中序与后序遍历序列构造二叉树 ⭐️ | 递归 |
| #652 寻找重复的子树 | 递归 |
| #103. 二叉树的锯齿形层序遍历 | 递归 |
| #112 判断路径和是否等于一个数 | 递归 |
| #437 统计路径和等于一个数的路径数量 | 递归 |
| #572 子树 | 递归 |
| #101 树的对称 | 递归 |
| #111 最小路径 | 递归 |
| #404 统计左叶子结点的和 | 递归 |
| #687 相同节点值的最大路径长度 | 递归 |
| #337 间隔遍历 | 递归 |
| #671 找出二叉树中第二小的节点 | 递归 |
| #637 一棵树每层节点的平均数 | 层次遍历 |
| #513 得到左下角的节点 | 层次遍历 |
| #699 修剪二叉查找树 | BST |
| #230 寻找二叉查找树的第 k 个元素 | BST |
| #538 把二叉查找树每个节点的值都加上比它大的节点的值 | BST |
| #235 二叉查找树的最近公共祖先 | BST |
| #236 二叉树的最近公共祖先 | BST |
| #108 从有序数组中构造二叉查找树 | BST |
| #109 根据有序链表构造平衡的二叉查找树 | BST |
| #653 在二叉查找树中寻找两个节点,使它们的和为一个给定值 | BST |
| #530 在二叉查找树中查找两个节点之差的最小绝对值 | BST |
| #501 寻找二叉查找树中出现次数最多的值 | BST |
| # 208 实现-trie-前缀树 | Trie |
| # 677 键值映射 | Trie |
// 自定义TreeNode节点
static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
栈和队列
| 题目 | 算法思想 |
|---|---|
| #232. 用栈实现队列 | |
| #225. 用队列实现栈 | |
| #155. 最小栈 | |
| #20. 有效的括号 ⭐️ | 辅助栈 |
| #32. 最长有效括号 ⭐️ | 栈/动态规划 |
| #739. 每日温度 | |
| #503. 下一个更大元素 II |
堆
| 题目 | 算法思想 |
|---|---|
哈希表
| 题目 | 算法思想 |
|---|---|
| #1. 两数之和 | |
| #217. 存在重复元素 | |
| #594. 最长和谐子序列 | |
| #128. 最长连续序列 |
字符串
| 题目 | 算法思想 |
|---|---|
| 242. 有效的字母异位词 ⭐️ | 排序/hashtable |
| 409. 最长回文串 ⭐️ | hashtable+一次遍历 |
| 205. 同构字符串 ⭐️ | hashtable/index |
| #647. 回文子串 ⭐️ | 中心扩展/动态规划 |
| #5. 最长回文子串 ⭐️ | 扩展中心 |
| #1371. 每个元音包含偶数次的最长子字符串 | 前缀和 + 状态压缩 |
| 字符串乘法计算 ⭐️ | |
| 剑指 Offer 05 替换空格 ⭐️ | 线性遍历 |
| 剑指 Offer 38 字符串的排列 ⭐️ | 回溯 |
| 判定子序列 | 二分查找/双指针 |
| 9. 回文数 ⭐️ | 数学/中心扩张 |
| #696. 计数二进制子串 |
位运算/大数
| 题目 | 算法思想 |
|---|---|
| 剑指 Offer 65. 不用加减乘除做加法 ⭐️ | 位运算 |
| #7. 整数反转 ⭐️ | 大数运算 |
| 大数求和 ⭐️ | 大数运算 |
| 461. 汉明距离 | |
| 136. 只出现一次的数字 | |
| 268. 丢失的数字 | |
| 260. 只出现一次的数字 III | |
| 190. 颠倒二进制位 | |
| 231. 2的幂 | |
| 342. 4的幂 | |
| 693. 交替位二进制数 | |
| 476. 数字的补数 | |
| 371. 两整数之和 | |
| 318. 最大单词长度乘积 | |
| 338. 比特位计数 |
数学
| 题目 | 算法思想 |
|---|---|
| n!末尾0的个数 ⭐️ | 因式分解 |
必刷算法题 ⭐️
| 题目 | 算法思想 |
|---|---|
| 手写生产者消费者 | |
| 线程轮流打印 | |
| IP地址与整数的相互转换 | |
| #69. x 的平方根 | |
| 手写阻塞队列 | |
题解
Template
- 简单
- 2022.01.02:
题目:
分析:
方法一:
代码:
#3. 无重复字符的最长子串
- 中等
- 2020.12.02:😭
题目:
给定一个字符串,请你找出其中不含有重复字符的最长子串的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
提示:
0 <= s.length <= 5 * 10^4
s 由英文字母、数字、符号和空格组成
分析:
public int lengthOfLongestSubstring(String s) {
// window计数器
HashMap<Character, Integer> window = new HashMap<>();
int left = 0;int right = 0;
int result = 0; // 记录结果
char[] sArray = s.toCharArray();
while (right < s.length()) {
// right扩大
Character c = sArray[right];
right++;
// 进行窗口内数据的一系列更新
window.put(c, window.getOrDefault(c, 0) + 1);
// 何时收缩? 当前字符计数值大于1时收缩
while (window.get(c) > 1) {
Character d = sArray[left];
left++;
// 进行窗口内数据的一系列更新
window.put(d, window.get(d) - 1);
}
// 收缩结束 已经没有重复字符(在这里更新答案)
result = Math.max(result, right - left);
}
return result;
}
这就是变简单了,连 need 和 valid 都不需要,而且更新窗口内数据也只需要简单的更新计数器 window 即可。
当 window[c] 值大于 1 时,说明窗口中存在重复字符,不符合条件,就该移动 left 缩小窗口了嘛。
唯一需要注意的是,在哪里更新结果 res 呢?我们要的是最长无重复子串,哪一个阶段可以保证窗口中的字符串是没有重复的呢?
这里和之前不一样,要在收缩窗口完成后更新 res,因为窗口收缩的 while 条件是存在重复元素,换句话说收缩完成后一定保证窗口中没有重复嘛。
#5. 最长回文子串
- 中等
- 2021.04.11:😎
题目:
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
分析:
方法一:扩展中心
寻找回文串的问题核心思想是:从中间开始向两边扩散来判断回文串。对于最长回文子串,就是这个意思:
for 0 <= i < len(s):
找到以 s[i] 为中心的回文串
更新答案
但是呢,我们刚才也说了,回文串的长度可能是奇数也可能是偶数,如果是abba这种情况,没有一个中心字符,上面的算法就没辙了。所以我们可以修改一下:
for 0 <= i < len(s):
找到以 s[i] 为中心的回文串
找到以 s[i] 和 s[i+1] 为中心的回文串
更新答案
但是这里的索引会越界,需要额外处理:先扩展不符合再缩小左右边界防止索引越界
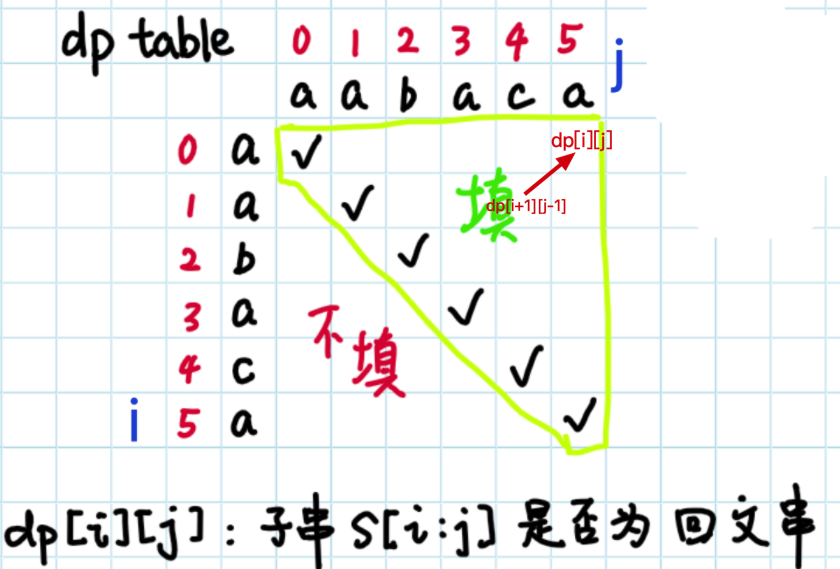
方法二:动态规划
状态:dp[i][j] 表示字符串s在[i,j]区间的子串是否是一个回文串。
状态转移方程:当 s[i] == s[j] && (j - i < 2 || dp[i + 1][j - 1]) 时,dp[i][j]=true,否则为false
这个状态转移方程是什么意思呢?
- case1: 当只有一个字符时,比如 a 自然是一个回文串。
- case2: 当有两个字符时,如果是相等的,比如 aa,也是一个回文串。
- case3: 当有三个及以上字符时,比如 ababa 这个字符记作串 1,把两边的 a 去掉,也就是 bab 记作串 2,可以看出只要串2是一个回文串,那么左右各多了一个 a 的串 1 必定也是回文串。所以当
s[i]==s[j]时,自然要看dp[i+1][j-1]是不是一个回文串。
遍历顺序:
s[i]==s[j]取决于状态 dp[i+1][j-1] 。
所以遍历顺序需要从下到上,从左到右。
代码:
// 方法一:扩展中心
private String res = "";
public String longestPalindrome(String s) {
for (int i = 0; i < s.length(); i++) {
// 找到以 s[i] 为中心的回文串
isPalindrome(s,i,i);
// 找到以 s[i] 和 s[i+1] 为中心的回文串
isPalindrome(s, i, i + 1);
}
return res;
}
// 寻找最长回文串函数
private void isPalindrome(String s, int left, int right) {
// ⚠️ 防止索引越界(先扩展指针,如果不符合了再缩小左右边界防止索引越界)
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)){
// 双向展开
left--;
right++;
}
// 更新res为s[left]和s[right]为中心的最长回文串
if((right-1)-(left+1)+1>res.length()){ // 因为在while循环中多扩展了一次,计算长度时记得收回
res = s.substring(left+1,right-1+1); // substring(int beginIndex, int endIndex),不包括endIndex
}
}
// 方法二 动态规划
public String longestPalindrome(String s) {
String res = "";
boolean[][] dp = new boolean[s.length()][s.length()];
// 注意遍历顺序
for (int i= s.length() - 1; i >= 0; i--){
for (int j = i; j < s.length(); j++){
if (s.charAt(i) == s.charAt(j)) {
if (j - i < 2) { // case1 和 case2
dp[i][j] = true;
if(j-i+1>res.length()) res = s.substring(i,j+1);
} else if (dp[i + 1][j - 1]) { // case3
dp[i][j] = true;
if(j-i+1>res.length()) res = s.substring(i,j+1);
}
}
}
}
return res;
}
#7. 整数反转
- 简单
- 2021.04.11:😎
题目:
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−2^31, 2^31 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123
输出:321
示例 2:
输入:x = -123
输出:-321
分析:
注意溢出:
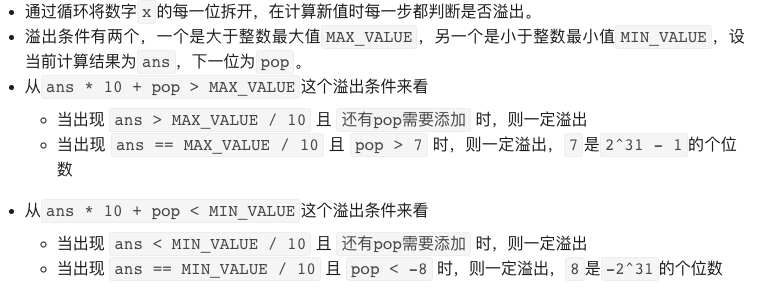
代码:
// 通过循环将数字 x 的每一位拆开,在计算新值的时候判断是否溢出
public int reverse(int x) {
int ans = 0; // 当前计算结果
while (x != 0) {
int pop = x%10; // 下一位pop
x = x/10;
// int 的范围 -2147483648 - 2147483647 , 所以判断7和-8
if (ans > Integer.MAX_VALUE/10 || (ans == Integer.MAX_VALUE/10 && pop > 7))
return 0;
if (ans < Integer.MIN_VALUE/10 || (ans == Integer.MIN_VALUE/10 && pop < -8))
return 0;
ans = ans * 10 + pop;
}
return ans;
}
9. 回文数
- 简单
- 2022.01.02:😎
题目:
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。例如,121 是回文,而 123 不是。
示例 1:
输入:x = 121
输出:true
示例 2:
输入:x = -121
输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10
输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
分析:
方法一:数学
如果是负数则一定不是回文数,直接返回 false
如果是正数,则将其倒序数值计算出来,然后比较和原数值是否相等
如果是回文数则相等返回 true,如果不是则不相等 false
比如 123 的倒序 321,不相等;121 的倒序 121,相等
方法二:回文串(字符串)
代码:
// 方法一
public boolean isPalindrome(int x) {
if(x < 0) return false;
int cur = 0;
int num = x;
while(num != 0) {
cur = cur * 10 + num % 10;
num /= 10;
}
return cur == x; //如果溢出了说明反转前后肯定不一样 那肯定不是回文数了
}
// 方法一优化版(实际上比较一半即可)
public boolean isPalindrome(int x) {
// 排除一些特殊情况,负数、10的倍数(0除外)
if (x < 0 || (x % 10 == 0 && x != 0))
return false;
int rev = 0;
while (rev < x) {
rev = x % 10 + rev * 10;
x /= 10; //一半就是 /= 后剩的值大小
}
return (rev == x || rev/10 == x);//长度为偶数时rev==x;奇数时候rev/10==x
}
// 方法二
public boolean isPalindrome(int x) {
String s = String.valueOf(x);
int left = s.length()/2;
int right = s.length()/2;
if(s.length()%2==0){
left = s.length()/2;
right = s.length()/2-1;
}
while(left>=0&&right<s.length()){
if(s.charAt(left)!=s.charAt(right)) return false;
left--;
right++;
}
return true;
}
#11. 盛最多水的容器
- medium
- 2019.09.13:😭
- 2019.09.15:😭 写成height[i++]<height[j–]了,呕
题目:
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
示例:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
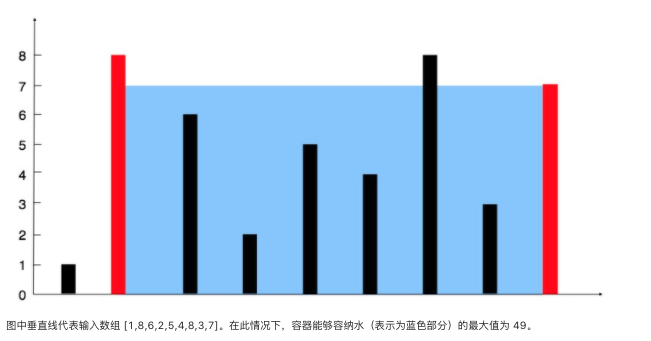
分析:双指针法
算法流程: 设置双指针 i,j 分别位于容器壁两端,根据规则移动指针(后续说明),并且更新面积最大值 res,直到 i == j 时返回 res。
“若向内移动短板,水槽的短板 min(h[i], h[j]) 可能变大,因此水槽面积 S(i, j)可能增大。若向内移动长板,水槽的短板 min(h[i], h[j]) 不变或变小,下个水槽的面积一定小于当前水槽面积。“其实可以加一句,无论是移动短板或者长板,我们都只关注移动后的新短板会不会变长,而每次移动的木板都只有三种情况,比原短板短,比原短板长,与原短板相等;如向内移动长板,对于新的木板:1.比原短板短,则新短板更短。2.与原短板相等或者比原短板长,则新短板不变。所以,向内移动长板,一定不能使新短板变长。
代码:
class Solution {
public int maxArea(int[] height) {
// 设置双指针 i,j 分别位于容器壁两端
int i = 0, j = height.length - 1, res = 0;
// 每次向内移动短板,并且更新面积最大值 res,直到 i == j 时返回 res。
while(i < j){
res = height[i] < height[j] ?
Math.max(res, (j - i) * height[i++]):
Math.max(res, (j - i) * height[j--]);
}
return res;
}
}
19. 删除链表的倒数第 N 个结点
- 中等
- 2021.11.25:
题目:
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
分析:
方法一:
快慢指针,让fast指针先走n步。
为了方便删除第一结点,最好加一个哨兵节点。
为了方便删除尾节点(n=1时),最好还是以fast!=null作为判断条件比较好,而不是fast.next!=null,不然不能使fast遍历到null。
代码:
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(-1);
dummy.next = head;
ListNode pre = dummy;
ListNode slow = head;
ListNode fast = head;
while(n!=0){
fast = fast.next;
n--;
}
while(fast!=null){ // 再简单一点的话slow指针可以删掉,直接pre.next = pre.next.next
pre = pre.next;
slow = slow.next;
fast = fast.next;
}
pre.next = slow.next;
return dummy.next;
}
#20. 有效的括号
- 简单
- 2021.03.20:😎
题目:
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
分析:
方法一:辅助栈法
- 算法原理
- 栈先入后出特点恰好与本题括号排序特点一致,即若遇到左括号入栈,遇到右括号时将对应栈顶左括号出栈,则遍历完所有括号后 stack 仍然为空;
- 建立哈希表 dic 构建左右括号对应关系:key 左括号,value 右括号;这样查询 2 个括号是否对应只需 O(1) 时间复杂度;建立栈 stack,遍历字符串 s 并按照算法流程一一判断。
- 算法流程
- 如果 c 是左括号,则入栈 push;
- 否则通过哈希表判断括号对应关系,若 stack 栈顶出栈括号 stack.pop() 与当前遍历括号 c 不对应,则提前返回 false。
-
提前返回false:

代码:
public boolean isValid(String s) {
Map<Character, Character> map = new HashMap<Character, Character>();
map.put('{', '}');
map.put('[', ']');
map.put('(', ')');
map.put('?', '?');
LinkedList<Character> stack = new LinkedList<Character>();
stack.add('?');
for (Character c : s.toCharArray()) {
if (map.containsKey(c)) {
stack.push(c);
}else if (map.get(stack.pop()) != c){
return false;
}
}
return stack.size() == 1; // s已左括号结尾也可以正常结束,但是stack会存在两个元素(?和左括号)。
}
21. 合并两个有序链表
- 简单
- 2021.11.22:😎
题目:
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
分析:迭代
head 有可能需要改动时,先增加一个 假head,返回的时候直接取 假head.next,这样就不需要为修改 head 增加一大堆逻辑了。
代码:
public ListNode mergeTwoLists(ListNode head1, ListNode head2) {
// 哨兵节点
ListNode dummyHead = new ListNode(-1);
ListNode cur = dummyHead;
while(head1!=null&&head2!=null){
if(head1.val<=head2.val){
cur.next = head1;
head1 = head1.next;
}else{
cur.next = head2;
head2 = head2.next;
}
cur = cur.next;
}
cur.next = head1==null?head2:head1;
return dummyHead.next;
}
#22. 括号生成
- 中等
- 2021.03.20:😭
题目:
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1
输出:["()"]
分析:
方法一:回溯
我们可以只在序列仍然保持有效时才添加 '(' or ')',可以通过跟踪到目前为止放置的左括号和右括号的数目来做到这一点,
- 如果左括号数量不大于 n,我们可以放一个左括号。
- 如果右括号数量小于左括号的数量,我们可以放一个右括号。
# 回溯模版
List<String> result = new ArrayList<String>();
public void backtrack(路径, 选择列表):
if (满足结束条件): // 递归出口
result.add(路径)
return;
for 选择 in 选择列表:
// 做选择
backtrack(路径, 选择列表)
// 撤销选择
代码:
private LinkedList<String> res = new LinkedList<>();
public List<String> generateParenthesis(int n) {
int[] arr = new int[2]; // 描述当前括号的状态[左括号数量,右括号数量]
StringBuilder list = new StringBuilder();
backtrack(arr,list,n);
return res;
}
private void backtrack(int[] arr, StringBuilder list,int max) {
if (arr[0]<arr[1]){ // 剪枝 左括号数量一定要大于右括号
return;
}
if (arr[0]==max&&arr[1]==max){
res.add(list.toString());
return;
}
// (
if (arr[0]<=max){
arr[0] = arr[0]+1;
list.append('(');
backtrack(arr,list,max);
list.deleteCharAt(list.length()-1);
arr[0] = arr[0]-1;
}
// )
if (arr[1]<=max){
arr[1] = arr[1]+1;
list.append(')');
backtrack(arr,list,max);
list.deleteCharAt(list.length()-1);
arr[1] = arr[1]-1;
}
}
}
#25. K 个一组翻转链表
- 困难
- 2021.03.20:😭
题目:
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
进阶:
你可以设计一个只使用常数额外空间的算法来解决此问题吗?
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
分析:
方法一:栈(容易理解)
k个一组压栈,然后出栈构建新链表:
- 注意原节点的next指针要置空,防止循环链表。
- 注意链表最后不足k的部分不需要翻转,这时候直接把栈底的节点连接到cur之后即可。
方法二:
步骤分解:
- 链表分区为已翻转部分+待翻转部分+未翻转部分
- 每次翻转前,要确定翻转链表的范围,这个必须通过 k 此循环来确定
- 需记录翻转链表前驱和后继,方便翻转完成后把已翻转部分和未翻转部分连接起来
- 初始需要两个变量 pre 和 end,pre 代表待翻转链表的前驱,end 代表待翻转链表的末尾
- 经过k此循环,end 到达末尾,记录待翻转链表的后继 next = end.next
- 翻转链表,然后将三部分链表连接起来,然后重置 pre 和 end 指针,然后进入下一次循环
- 特殊情况,当翻转部分长度不足 k 时,在定位 end 完成后,end==null,已经到达末尾,说明题目已完成,直接返回即可

代码:
// 方法一
public ListNode reverseKGroup(ListNode head, int k) {
if (head == null) {
return null;
}
Stack<ListNode> stack = new Stack<>();
ListNode dummyNode = new ListNode(-1);
ListNode cur = dummyNode;
while (head!= null || !stack.isEmpty()) {
// k个一组压栈
for (int i = 0; i < k; i++) {
// 注意链表最后不足k的部分不需要翻转,这时候直接把栈底的节点连接到cur之后即可。
if (head == null) {
while(!stack.isEmpty()){
ListNode node = stack.pop();
if(stack.size()==0){
cur.next = node;
}
}
break;
}
stack.push(head);
head = head.next;
}
// 出栈构建新链表
while (!stack.isEmpty()) {
ListNode node = stack.pop();
cur.next = node;
node.next = null;
cur = node;
}
}
return dummyNode.next;
}
// 方法二
public ListNode reverseKGroup(ListNode head, int k) {
if (head == null || head.next == null){
return head;
}
//定义一个假的节点。
ListNode dummy=new ListNode(0);
//假节点的next指向head。
// dummy->1->2->3->4->5
dummy.next=head;
//初始化pre和end都指向dummy。pre指每次要翻转的链表的头结点的上一个节点。end指每次要翻转的链表的尾节点
ListNode pre=dummy;
ListNode end=dummy;
while(end.next!=null){
//循环k次,找到需要翻转的链表的结尾,这里每次循环要判断end是否等于空,因为如果为空,end.next会报空指针异常。
//dummy->1->2->3->4->5 若k为2,循环2次,end指向2
for(int i=0;i<k;i++){
if(end== null) break;
end=end.next;
}
//如果end==null,即需要翻转的链表的节点数小于k,不执行翻转。
if(end==null){
break;
}
//先记录下end.next,方便后面链接链表
ListNode next=end.next;
//然后断开链表
end.next=null;
//记录下要翻转链表的头节点
ListNode start=pre.next;
//翻转链表,pre.next指向翻转后的链表。1->2 变成2->1。 dummy->2->1
pre.next=reverse(start);
//翻转后头节点变到最后。通过.next把断开的链表重新链接。
start.next=next;
//将pre换成下次要翻转的链表的头结点的上一个节点。即start
pre=start;
//翻转结束,将end置为下次要翻转的链表的头结点的上一个节点。即start
end=start;
}
return dummy.next;
}
//链表翻转
// 例子: head: 1->2->3->4
public ListNode reverse(ListNode head) {
//单链表为空或只有一个节点,直接返回原单链表
if (head == null){
return null;
}
//前一个节点指针
ListNode preNode = null;
//当前节点指针
ListNode curNode = head;
//下一个节点指针
ListNode nextNode = null;
while (curNode != null){
nextNode = curNode.next;//nextNode 指向下一个节点,保存当前节点后面的链表。
curNode.next=preNode;//将当前节点next域指向前一个节点 null<-1<-2<-3<-4
preNode = curNode;//preNode 指针向后移动。preNode指向当前节点。
curNode = nextNode;//curNode指针向后移动。下一个节点变成当前节点
}
return preNode;
}
#26. 删除排序数组中的重复项
- Easy
- 2019.08.30:😭
题目:
给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
分析:双指针法
数组完成排序后,我们可以放置两个指针 i 和 j,其中 i 是慢指针,而 j 是快指针。慢指针 i 用于记录最后一次出现的数字,快指针 j 用于遍历数组的每一个元素,并把未出现过的数赋值给第 i+1 个元素。
只要 nums[i] = nums[j],我们就增加 j 以跳过重复项。当我们遇到 nums[j] 不等于 nums[i],跳过重复项的运行已经结束,因此我们必须把它(nums[j])的值复制到 nums[i + 1]。然后递增 i,接着我们将再次重复相同的过程,直到 j 到达数组的末尾为止。
复杂度分析
时间复杂度:O(n)O(n),假设数组的长度是 n,那么 i 和 j 分别最多遍历 n 步。
空间复杂度:O(1)O(1)。
代码:
public int removeDuplicates(int[] nums) {
if (nums.length == 0) return 0;
int i = 0;
for (int j = 1; j < nums.length; j++) {
if (nums[j] != nums[i]) {
nums[++i]=nums[j];
}
}
return i + 1;
}
#32. 最长有效括号
- 困难
- 2021.03.20:😭
题目:
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
分析:
方法一:动态规划
方法一:栈
通过栈,我们可以在遍历给定字符串的过程中去判断到目前为止扫描的子串的有效性,同时能得到最长有效括号的长度。具体做法是我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」,这样的做法主要是考虑了边界条件的处理,栈里其他元素维护左括号的下标:
- 对于遇到的每个
(,我们将它的下标放入栈中 - 对于遇到的每个
),我们先弹出栈顶元素表示匹配了当前右括号:- 如果栈为空,说明当前的右括号为没有被匹配的右括号,我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
- 如果栈不为空,当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
我们从前往后遍历字符串并更新答案即可。需要注意的是,如果一开始栈为空,第一个字符为左括号的时候我们会将其放入栈中,这样就不满足提及的「最后一个没有被匹配的右括号的下标」,为了保持统一,我们在一开始的时候往栈中放入一个值为 −1 的元素。
代码:
// 栈
public int longestValidParentheses(String s) {
int res = 0;
Deque<Integer> stack = new LinkedList<Integer>();
stack.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
stack.pop();
if (stack.empty()) {
stack.push(i);
} else {
res = Math.max(res, i - stack.peek());
}
}
}
return res;
}
#34. 在排序数组中查找元素的第一个和最后一个位置
- 中等
- 2020.11.25:😭
题目:
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]
分析:
方法一:二分查找左右边界
代码:
class Solution {
public int[] searchRange(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
// 寻找左边界
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] == target) {
right = mid - 1;
}
}
// 越界或不存在补丁
int res1 = left;
if (left >= nums.length || nums[left] != target) {
res1 = -1;
}
// 寻找右边界
left = 0;
right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] == target) {
left = mid + 1;
}
}
// 越界或不存在补丁
int res2 = right;
if (right < 0 || nums[right] != target) {
res2 = -1;
}
return new int[]{res1, res2};
}
}
#46. 全排列
- 中等
- 2020.11.17:😭
题目:
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
分析:
我们在高中的时候就做过排列组合的数学题,我们也知道 n 个不重复的数,全排列共有 n! 个。
PS:为了简单清晰起见,我们这次讨论的全排列问题不包含重复的数字。
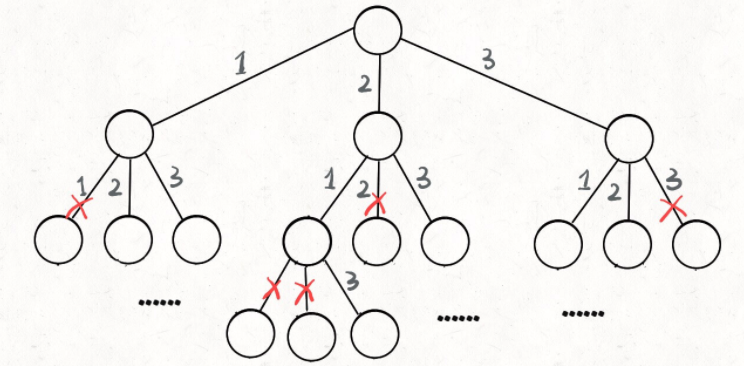
那么我们当时是怎么穷举全排列的呢?比方说给三个数 [1,2,3],你肯定不会无规律地乱穷举,一般是这样:
先固定第一位为 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位变成 3,第三位就只能是 2 了;然后就只能变化第一位,变成 2,然后再穷举后两位……
其实这就是回溯算法,我们高中无师自通就会用,或者有的同学直接画出如下这棵回溯树:
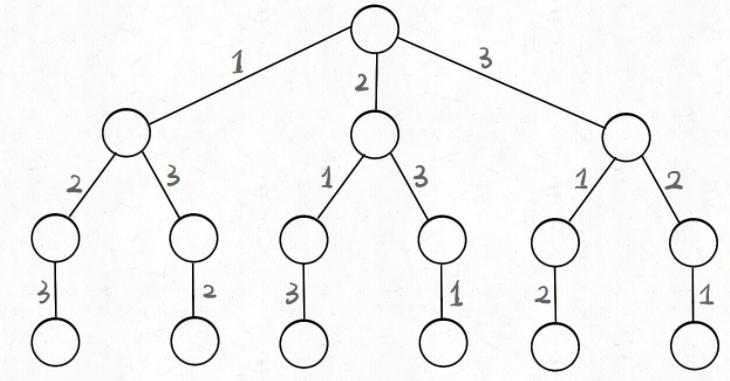
只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。
为啥说这是决策树呢,因为你在每个节点上其实都在做决策。比如说你站在下图的红色节点上:
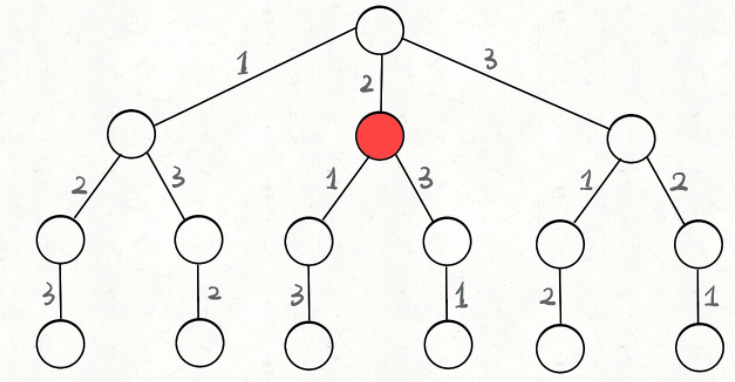
你现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
现在可以解答开头的几个名词:[2] 就是「路径」,记录你已经做过的选择;[1,3] 就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层,在这里就是选择列表为空的时候。
如果明白了这几个名词,可以把「路径」和「选择」列表作为决策树上每个节点的属性,比如下图列出了几个节点的属性:
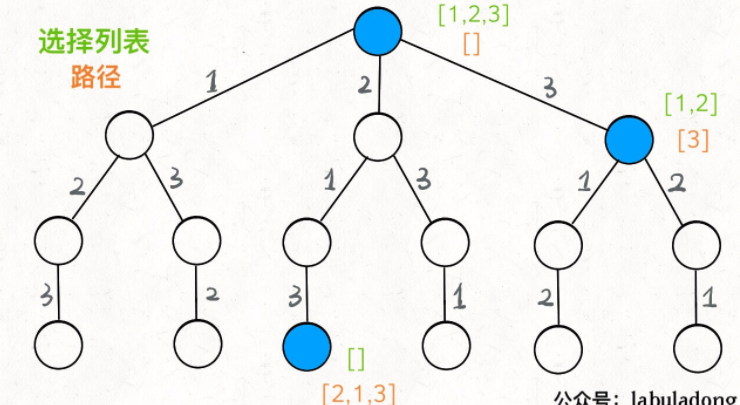
我们定义的 backtrack 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层,其「路径」就是一个全排列。
再进一步,如何遍历一棵树?这个应该不难吧。回忆一下之前「学习数据结构的框架思维」写过,各种搜索问题其实都是树的遍历问题,而多叉树的遍历框架就是这样:
void traverse(TreeNode root) {
for (TreeNode child : root.childern)
// 前序遍历需要的操作
traverse(child);
// 后序遍历需要的操作
}
而所谓的前序遍历和后序遍历,他们只是两个很有用的时间点,我给你画张图你就明白了:
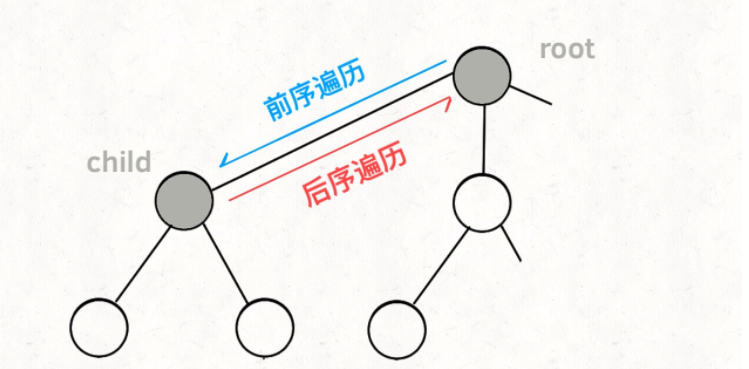
前序遍历的代码在进入某一个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在树上游走要正确维护节点的属性,那么就要在这两个特殊时间点搞点动作:
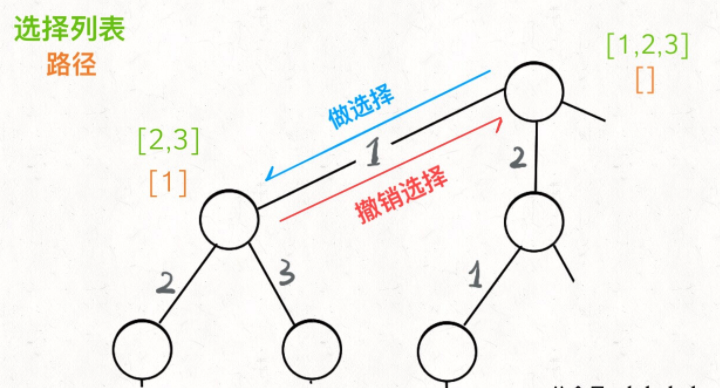
现在,你是否理解了回溯算法的这段核心框架?
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
我们只要在递归之前做出选择,在递归之后撤销刚才的选择,就能正确得到每个节点的选择列表和路径。
下面,直接看全排列代码:
class Solution {
private List<List<Integer>> res = new LinkedList<>();
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
public List<List<Integer>> permute(int[] nums) {
// 记录「路径」
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return res;
}
// 路径:记录在 track 中
// 选择列表:nums 中不存在于 track 的那些元素
// 结束条件:nums 中的元素全都在 track 中出现
public void backtrack(int[] nums, LinkedList<Integer> track) {
// 触发结束条件
if (track.size() == nums.length) {
// 就是你 list 是个引用类型,你把它 push 到 res 里面之后,其实 push 的是同一个玩意,到最后输出的全是空的。
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 判断何时才能前进,排除不合法的选择
if (!track.contains(nums[i])){
// 做选择
track.add(nums[i]);
// 进入下一层决策树
backtrack(nums, track);
// 取消选择
track.removeLast();
}
}
}
}
我们这里稍微做了些变通,没有显式记录「选择列表」,而是通过 nums 和 track 推导出当前的选择列表:
至此,我们就通过全排列问题详解了回溯算法的底层原理。当然,这个算法解决全排列不是很高效,因为对链表使用 contains 方法需要 O(N) 的时间复杂度。有更好的方法通过交换元素达到目的,但是难理解一些,这里就不写了,有兴趣可以自行搜索一下。
但是必须说明的是,不管怎么优化,都符合回溯框架,而且时间复杂度都不可能低于 O(N!),因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点,不像动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
#51. N 皇后
- 困难
- 2020.11.17:😭
题目:
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
输入:4
输出:[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
提示:
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
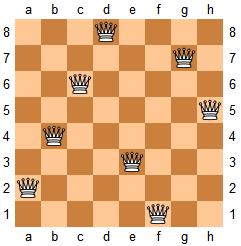
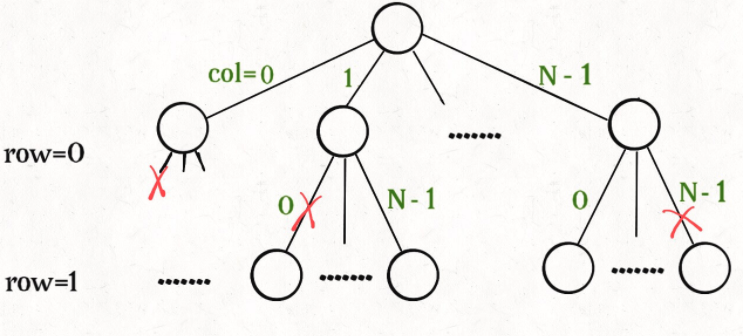
分析:
这个问题本质上跟全排列问题差不多,决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
直接套用框架:
private List<List<String>> res = new LinkedList<>();
/* 输入棋盘边长 n,返回所有合法的放置 */
public List<List<String>> solveNQueens(int n) {
// '.' 表示空,'Q' 表示皇后,初始化空棋盘。
char[][] board = new char[n][n];
//初始化数组
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
board[i][j] = '.';
backtrack(board, 0);
return res;
}
// 路径:board 中小于 row 的那些行都已经成功放置了皇后
// 选择列表:第 row 行的所有列都是放置皇后的选择
// 结束条件:row 超过 board 的最后一行
public void backtrack(char[][] board, int row) {
// 触发结束条件,最后一行都走完了,说明找到了一组,把它加入到集合res中
if (row == board.length) {
res.add(construct(board));
return;
}
// 遍历选择列表
for (int col = 0; col < board.length; col++) {
// 判断何时前进,排除不合法选择
if (isValid(board, row, col)) {
// 做选择
board[row][col] = 'Q';
// backtrack(路径,选择列表)
backtrack(board, row + 1);
// 撤销选择
board[row][col] = '.';
}
}
}
//把数组转为list
private List<String> construct(char[][] board) {
List<String> path = new ArrayList<>();
for (int i = 0; i < board.length; i++) {
path.add(new String(board[i]));
}
return path;
}
这部分主要代码,其实跟全排列问题差不多,isValid 函数的实现也很简单:
/* 是否可以在 board[row][col] 放置皇后? */
private boolean isValid(char[][] board, int row, int col) {
//判断当前列有没有皇后,因为他是一行一行往下走的,
//我们只需要检查走过的行数即可,通俗一点就是判断当前
//坐标位置的上面有没有皇后
for (int i = 0; i < row; i++) {
if (board[i][col] == 'Q') {
return false;
}
}
//判断当前坐标的右上角有没有皇后
for (int i = row - 1, j = col + 1; i >= 0 && j < board.length; i--, j++) {
if (board[i][j] == 'Q') {
return false;
}
}
//判断当前坐标的左上角有没有皇后
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') {
return false;
}
}
return true;
}
函数 backtrack 依然像个在决策树上游走的指针,通过 row 和 col 就可以表示函数遍历到的位置,通过 isValid 函数可以将不符合条件的情况剪枝:
如果直接给你这么一大段解法代码,可能是懵逼的。但是现在明白了回溯算法的框架套路,还有啥难理解的呢?无非是改改做选择的方式,排除不合法选择的方式而已,只要框架存于心,你面对的只剩下小问题了。
当 N = 8 时,就是八皇后问题,数学大佬高斯穷尽一生都没有数清楚八皇后问题到底有几种可能的放置方法,但是我们的算法只需要一秒就可以算出来所有可能的结果。
不过真的不怪高斯。这个问题的复杂度确实非常高,看看我们的决策树,虽然有 isValid 函数剪枝,但是最坏时间复杂度仍然是 O(N^(N+1)),而且无法优化。如果 N = 10 的时候,计算就已经很耗时了。
有的时候,我们并不想得到所有合法的答案,只想要一个答案,怎么办呢?比如解数独的算法,找所有解法复杂度太高,只要找到一种解法就可以。
其实特别简单,只要稍微修改一下回溯算法的代码即可:
// 函数找到一个答案后就返回 true
bool backtrack(vector<string>& board, int row) {
// 触发结束条件
if (row == board.size()) {
res.push_back(board);
return true;
}
...
for (int col = 0; col < n; col++) {
...
board[row][col] = 'Q';
if (backtrack(board, row + 1))
return true;
board[row][col] = '.';
}
return false;
}
这样修改后,只要找到一个答案,for 循环的后续递归穷举都会被阻断。
#53. 最大子序和
- 简单
- 2020.12.15:
题目:
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
分析:
其实第一次看到这道题,我首先想到的是滑动窗口算法,因为我们前文说过嘛,滑动窗口算法就是专门处理子串/子数组问题的,这里不就是子数组问题么?
但是,稍加分析就发现,这道题还不能用滑动窗口算法,因为数组中的数字可以是负数。
滑动窗口算法无非就是双指针形成的窗口扫描整个数组/子串,但关键是,你得清楚地知道什么时候应该移动右侧指针来扩大窗口,什么时候移动左侧指针来减小窗口。
而对于这道题目,你想想,当窗口扩大的时候可能遇到负数,窗口中的值也就可能增加也可能减少,这种情况下不知道什么时机去收缩左侧窗口,也就无法求出「最大子数组和」。
解决这个问题需要动态规划技巧,但是 dp 数组的定义比较特殊。按照我们常规的动态规划思路,一般是这样定义 dp 数组:
nums[0..i] 中的「最大的子数组和」为 dp[i]。
如果这样定义的话,整个 nums 数组的「最大子数组和」就是 dp[n-1]。如何找状态转移方程呢?按照数学归纳法,假设我们知道了 dp[i-1],如何推导出 dp[i] 呢?
如下图,按照我们刚才对 dp 数组的定义,dp[i] = 5 ,也就是等于 nums[0..i] 中的最大子数组和
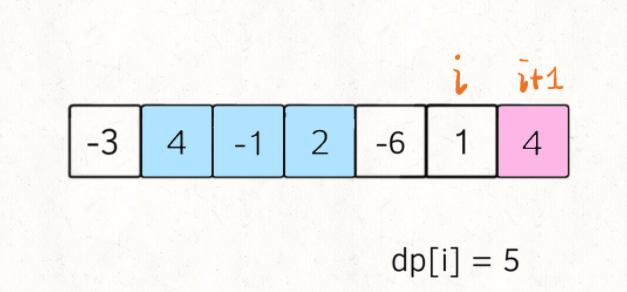
那么在上图这种情况中,利用数学归纳法,你能用 dp[i] 推出 dp[i+1] 吗?
实际上是不行的,因为子数组一定是连续的,按照我们当前 dp 数组定义,并不能保证 nums[0..i] 中的最大子数组与 nums[i+1] 是相邻的,也就没办法从 dp[i] 推导出 dp[i+1]。
所以说我们这样定义 dp 数组是不正确的,无法得到合适的状态转移方程。对于这类子数组问题,我们就要重新定义 dp 数组的含义:
⚠️ 以 nums[i] 为结尾的「最大子数组和」为 dp[i]。
这种定义之下,想得到整个 nums 数组的「最大子数组和」,不能直接返回 dp[n-1],而需要遍历整个 dp 数组:
int res = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
res = Math.max(res, dp[i]);
}
return res;
依然使用数学归纳法来找状态转移关系:假设我们已经算出了 dp[i-1],如何推导出 dp[i] 呢?
可以做到,dp[i] 有两种「选择」,要么与前面的相邻子数组连接,形成一个和更大的子数组;要么不与前面的子数组连接,自成一派,自己作为一个子数组。
如何选择?既然要求「最大子数组和」,当然选择结果更大的那个啦:
// 要么自成一派,要么和前面的子数组合并
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
综上,我们已经写出了状态转移方程,就可以直接写出解法了:
int maxSubArray(int[] nums) {
int n = nums.length;
int res = nums[0];
if (n == 0) return 0;
int[] dp = new int[n];
// base case
// 第一个元素前面没有子数组
dp[0] = nums[0];
// 状态转移方程
for (int i = 1; i < n; i++) {
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
res = Math.max(res, dp[i]);
}
return res;
}
以上解法时间复杂度是 O(N),空间复杂度也是 O(N),较暴力解法已经很优秀了,不过注意到 dp[i] 仅仅和 dp[i-1] 的状态有关,那么我们可以进行「状态压缩」,将空间复杂度降低:
int maxSubArray(int[] nums) {
int n = nums.length;
if (n == 0) return 0;
// base case
int dp_0 = nums[0];
int dp_1 = 0, res = dp_0;
for (int i = 1; i < n; i++) {
// dp[i] = max(nums[i], nums[i] + dp[i-1])
dp_1 = Math.max(nums[i], nums[i] + dp_0);
dp_0 = dp_1;
// 顺便计算最大的结果
res = Math.max(res, dp_1);
}
return res;
}
#69. x 的平方根
- 简单
- 2021.04.11:😎
题目:
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
分析:
方法一:二分查找
分析单调性:注意到题目中给出的例 2,小数部分将被舍去。我们就知道了,如果一个数 a 的平方大于 x ,那么 a 一定不是 x 的平方根。我们下一轮需要在 [0..a−1] 区间里继续查找 x 的平方根。
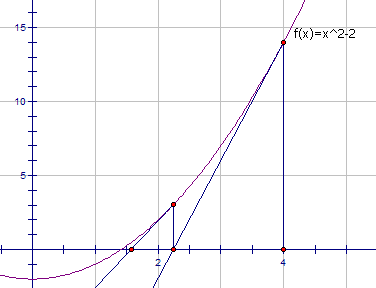
方法二:牛顿迭代法
这种方法可以很有效地求出根号 aa 的近似值:首先随便猜一个近似值 xx,然后不断令 xx 等于 xx 和 a/xa/x 的平均数,迭代个六七次后 xx 的值就已经相当精确了。
例如,我想求根号 2 等于多少。假如我猜测的结果为 4,虽然错的离谱,但你可以看到使用牛顿迭代法后这个值很快就趋近于根号 2 了:
( 4 + 2/ 4 ) / 2 = 2.25
( 2.25 + 2/ 2.25 ) / 2 = 1.56944..
( 1.56944..+ 2/1.56944..) / 2 = 1.42189..
( 1.42189..+ 2/1.42189..) / 2 = 1.41423..
….

代码:
// 二分查找
public int mySqrt(int x) {
int l = 0, r = x, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long) mid * mid <= x) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
// 牛顿迭代法
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
double C = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + C / x0);
if (Math.abs(x0 - xi) < 1e-7) {
break;
}
x0 = xi;
}
return (int) x0;
}
#72. 编辑距离
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int[][] dp = new int[m + 1][n + 1];
// base case
for (int i = 0; i <= m; i++) {
dp[i][0] = i;
}
for (int j = 0; j <= n; j++) {
dp[0][j] = j;
}
// 自底向上求解
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1))
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1),
dp[i - 1][j - 1] + 1);
}
}
// 储存着整个 s1 和 s2 的最小编辑距离
return dp[m][n];
}
}
#75. 颜色分类
- easy
- 2019.08.28:😭
题目:
分析:
代码:
#76. 最小覆盖子串
- 困难
- 2020.12.02:😭
- 2021.03.06:😭 收缩逻辑混乱,何时更新最小覆盖子串。
题目:
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
提示:
1) 1 <= s.length, t.length <= 105
2) s 和 t 由英文字母组成
分析:
方法一:滑动窗口
滑动窗口算法的思路是这样:
1、我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引左闭右开区间 [left, right) 称为一个「窗口」。
2、我们先不断地增加 right 指针扩大窗口 [left, right),直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
3、此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right),直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
4、重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解,也就是最短的覆盖子串。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动,这就是「滑动窗口」这个名字的来历。
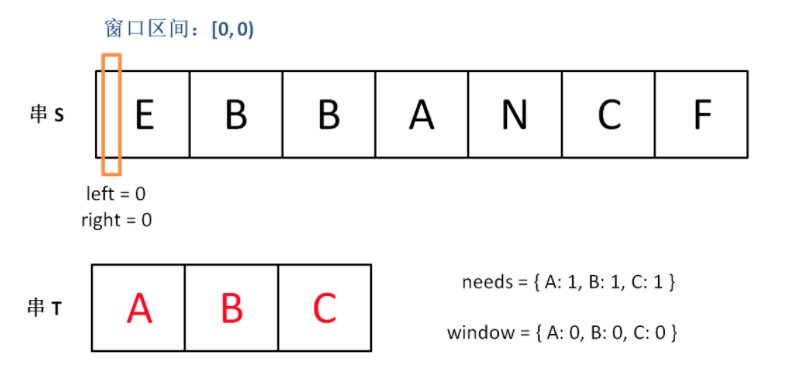
下面画图理解一下,needs 和 window 相当于计数器,分别记录 T 中字符出现次数和「窗口」中的相应字符的出现次数。
初始状态:
增加 right,直到窗口 [left, right] 包含了 T 中所有字符:
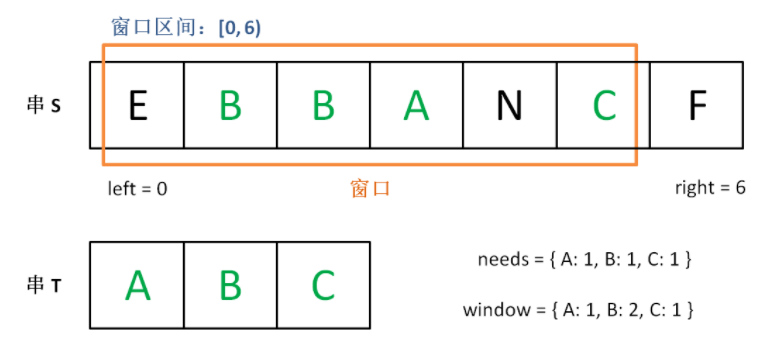
现在开始增加 left,缩小窗口 [left, right]。
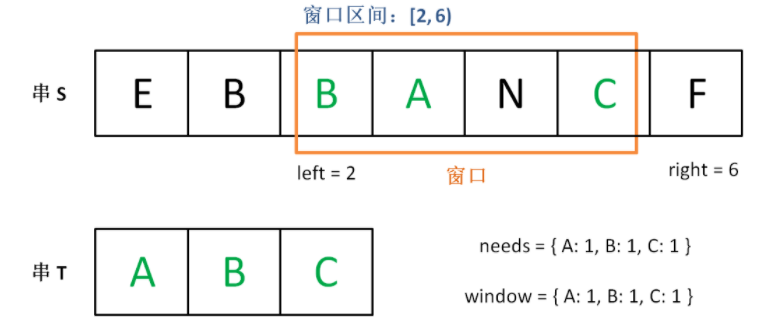
直到窗口中的字符串不再符合要求,left 不再继续移动。
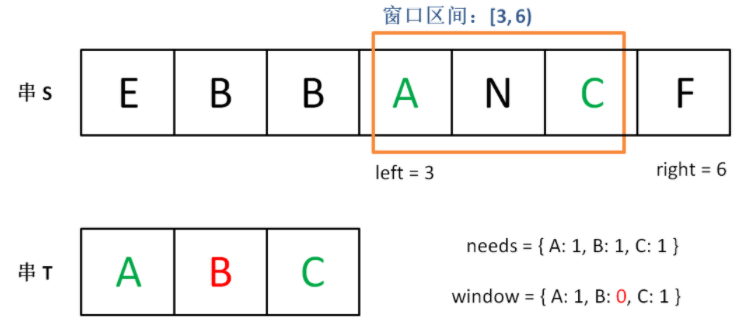
之后重复上述过程,先移动 right,再移动 left…… 直到 right 指针到达字符串 S 的末端,算法结束。
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。现在我们来看看这个滑动窗口代码框架怎么用:
首先,初始化 window 和 need 两个哈希表,记录窗口中的字符和需要凑齐的字符:
HashMap<Character, Integer> need = new HashMap<>();
for (char key : t.toCharArray()) {
// Map集合中有这个key时,就使用这个key对应的value值,如果没有就使用默认值defaultValue
need.put(key, need.getOrDefault(key, 0) + 1);
}
HashMap<Character, Integer> window = new HashMap<>();// 用于记录「窗口」中的相应字符的出现次数
然后,使用 left 和 right 变量初始化窗口的两端,不要忘了,区间 [left, right) 是左闭右开的,所以初始情况下窗口没有包含任何元素:
int left = 0, right = 0;
int valid = 0;
while (right < s.length()) {
// 开始滑动
}
其中 valid 变量表示窗口中满足 need 条件的字符个数,如果 valid 和 need.size 的大小相同,则说明窗口已满足条件,已经完全覆盖了串 T。
现在开始套模板,只需要思考以下四个问题:
1、当移动 right 扩大窗口,即加入字符时,应该更新哪些数据?
2、什么条件下,窗口应该暂停扩大,开始移动 left 缩小窗口?
3、当移动 left 缩小窗口,即移出字符时,应该更新哪些数据?
4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新?
如果一个字符进入窗口,应该增加 window 计数器;如果一个字符将移出窗口的时候,应该减少 window 计数器;当 valid 满足 need 时应该收缩窗口;应该在收缩窗口的时候更新最终结果。
下面是完整代码:
public String minWindow(String s, String t) {
// 需要的字符散列表 全部初始化为1(表示需要)
HashMap<Character, Integer> need = new HashMap<>();
for (char key : t.toCharArray()) {
// Map集合中有这个key时,就使用这个key对应的value值,如果没有就使用默认值defaultValue
need.put(key, need.getOrDefault(key, 0) + 1);
}
HashMap<Character, Integer> window = new HashMap<>();// 用于记录「窗口」中的相应字符的出现次数
int left = 0;
int right = 0;
int valid = 0; // 表示窗口中满足need条件的字符个数
// 记录最小覆盖子串的起始索引及长度
int start = 0;
int len = Integer.MAX_VALUE;
char[] sArray = s.toCharArray();
// 开始滑动
while(right<sArray.length){
// c 是将移入窗口的字符
char c = sArray[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
if (need.containsKey(c)){
window.put(c,window.getOrDefault(c,0)+1);
// ⚠️ 这个好像是 Java 包装类的原因,不能用等号而要用 equals 方法
if (window.get(c).equals(need.get(c))){
valid++;
}
}
// 判断左侧窗口是否要收缩
while(valid==need.size()){
// 在这里更新最小覆盖子串
if (right-left<len){
start = left;
len = right-left;
}
// d 是将移出窗口的字符
char d = sArray[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
if (need.containsKey(d)){
if (window.get(d).equals(need.get(d))){
valid--;
}
window.put(d,window.get(d)-1);
}
}
}
// 返回最小覆盖子串
return len==Integer.MAX_VALUE?"":s.substring(start,start+len);
}
需要注意的是,当我们发现某个字符在 window 的数量满足了 need 的需要,就要更新 valid,表示有一个字符已经满足要求。而且,你能发现,两次对窗口内数据的更新操作是完全对称的。
当 valid == need.size() 时,说明 T 中所有字符已经被覆盖,已经得到一个可行的覆盖子串,现在应该开始收缩窗口了,以便得到「最小覆盖子串」。
移动 left 收缩窗口时,窗口内的字符都是可行解,所以应该在收缩窗口的阶段进行最小覆盖子串的更新,以便从可行解中找到长度最短的最终结果。
至此,应该可以完全理解这套框架了,滑动窗口算法又不难,就是细节问题让人烦得很。以后遇到滑动窗口算法,你就按照这框架写代码,保准没有 bug,还省事儿。
83. 删除排序链表中的重复元素
- 简单
- 2021.11.25:😎
题目:
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除所有重复的元素,使每个元素 只出现一次。
返回同样按升序排列的结果链表。
分析:
方法一:
由于给定的链表是排好序的,因此重复的元素在链表中出现的位置是连续的,因此我们只需要对链表进行一次遍历,就可以删除重复的元素。
代码:
public ListNode deleteDuplicates(ListNode head) {
if(head==null) return null;
ListNode dummyHead = new ListNode(Integer.MAX_VALUE);
dummyHead.next = head;
ListNode pre = dummyHead;
ListNode cur = head;
while(cur!=null){
if(pre.val==cur.val){
pre.next = cur.next;
cur = cur.next;
}else{
pre = cur;
cur = cur.next;
}
}
return dummyHead.next;
}
#88. 合并两个有序数组
- Easy
- 2019.08.30:😭
- 2021.03.05 :😭 循环终止条件想不出(双指针 / 从后往前 )
题目:
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
分析:双指针
方法一 : 合并后排序
直觉
最朴素的解法就是将两个数组合并之后再排序。该算法只需要一行(Java是2行),时间复杂度较差,为O((n + m)log(n + m)。这是由于这种方法没有利用两个数组本身已经有序这一点。
复杂度分析:
时间复杂度 : O((n+m)log(n+m))
空间复杂度 : O(1)
方法二 : 双指针 / 从前往后
一般而言,对于有序数组可以通过 双指针法达到O(n + m)的时间复杂度。
最直接的算法实现是将指针p1 置为 nums1的开头, p2为 nums2的开头,在每一步将最小值放入输出数组中。
由于 nums1 是用于输出的数组,需要将nums1中的前m个元素放在其他地方,也就需要 O(m) 的空间复杂度。
复杂度分析:
时间复杂度 : O(n+m)
空间复杂度 : O(m)
⭐️方法三 : 双指针 / 从后往前
方法二已经取得了最优的时间复杂度O(n + m),但需要使用额外空间。这是由于在从头改变nums1的值时,需要把nums1中的元素存放在其他位置。
如果我们从结尾开始改写 nums1 的值又会如何呢?这里没有信息,因此不需要额外空间。
这里的指针 p 用于追踪添加元素的位置。
复杂度分析:
时间复杂度 : O(n + m)
空间复杂度 : O(1)
代码:
// 方法一
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
System.arraycopy(nums2, 0, nums1, m, n);
Arrays.sort(nums1);
}
}
// 方法二
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// 由于 nums1 是用于输出的数组,需要将nums1中的前m个元素放在其他地方.
int [] nums1_copy = new int[m];
System.arraycopy(nums1, 0, nums1_copy, 0, m);
// 设置 nums1_copy 和 nums2 的指针
int p1 = 0;
int p2 = 0;
// 设置 nums1 的指针
int p = 0;
// 比较 nums1_copy 和 nums2 中的元素,并把小的元素放入 nums1
while ((p1 < m) && (p2 < n))
nums1[p++] = (nums1_copy[p1] < nums2[p2]) ? nums1_copy[p1++] : nums2[p2++];
// 如果还有元素未被放入 nums1
if (p1 < m)
System.arraycopy(nums1_copy, p1, nums1, p1 + p2, m + n - p1 - p2);
if (p2 < n)
System.arraycopy(nums2, p2, nums1, p1 + p2, m + n - p1 - p2);
}
}
// ⭐️方法三
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// 设置 nums1 和 nums2 的指针
int p1 = m - 1;
int p2 = n - 1;
// 设置 合并后nums1 的指针
int p = m + n - 1;
// 比较 nums1 和 nums2 中的元素,并把大的元素放入 nums1 [从尾部放入]
while(p1>=0&&p2>=0){
if(nums1[p1]<nums2[p2]){
nums1[p] = nums2[p2];
p2--;
p--;
}else{
nums1[p] = nums1[p1];
p1--;
p--;
}
}
// 如果 nums2 还有剩余,全部放入 nums1 的顶端 (如果剩余的是nums1则p2=-1,等于无变化)
for(int i=0;i<=p2;i++){
nums1[i] = nums2[i];
}
}
}
#91. 解码方法
- 中等
- 2021.04.13:
题目:
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
'A' -> 1 'B' -> 2 ... 'Z' -> 26
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"11106" 可以映射为:
"AAJF" ,将消息分组为 (1 1 10 6)
"KJF" ,将消息分组为 (11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 "06" 不能映射为 "F" ,这是由于 "6" 和 "06" 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = "12"
输出:2
解释:它可以解码为 "AB"(1 2)或者 "L"(12)。
示例 2:
输入:s = "226"
输出:3
解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
分析:动态规划
这其实是一道字符串类的动态规划题,不难发现对于字符串 s 的某个位置 i 而言,我们只关心「位置 i 自己能否形成独立 item 」和「位置 i 能够与上一位置(i-1)能否形成 item」,而不关心 i-1 之前的位置。
有了以上分析,我们可以从前往后处理字符串 s,使用一个数组记录以字符串 s 的每一位作为结尾的解码方案数。即定义 f[i] 为考虑前 i 个字符的解码方案数。对于字符串 s 的任意位置 i 而言,其存在三种情况:
- 只能由位置 i 的单独作为一个 item,设为 a,转移的前提是 a 的数值范围为
[1,9],转移逻辑为f[i] = f[i - 1]。 - 只能由位置 i 的与前一位置(i-1)共同作为一个 item,设为 b,转移的前提是 b 的数值范围为
[10,26],转移逻辑为f[i] = f[i - 2]。 - 位置 i 既能作为独立 item 也能与上一位置形成 item,转移逻辑为
f[i] = f[i - 1] + f[i - 2]。
由此得出状态转移方程:
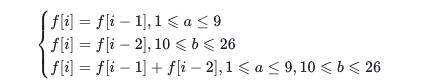
其他细节:由于题目存在前导零,而前导零属于无效 item。可以进行特判,但个人习惯往字符串头部追加空格作为哨兵,追加空格既可以避免讨论前导零,也能使下标从 1 开始,简化 f[i-1] 等负数下标的判断。
代码:
class Solution {
public int numDecodings(String s) {
int n = s.length();
s = " " + s;
char[] arr = s.toCharArray();
int[] dp = new int[n + 1];
f[0] = 1;
for (int i = 1; i <= n; i++) {
// a : 代表「当前位置」单独形成 item
// b : 代表「当前位置」与「前一位置」共同形成 item
int a = arr[i] - '0', b = (arr[i - 1] - '0') * 10 + (arr[i] - '0');
// 如果 a 属于有效值,那么 f[i] 可以由 f[i - 1] 转移过来
if (1 <= a && a <= 9) dp[i] = dp[i - 1];
// 如果 b 属于有效值,那么 f[i] 可以由 f[i - 2] 或者 f[i - 1] & f[i - 2] 转移过来
if (10 <= b && b <= 26) dp[i] += dp[i - 2];
}
return dp[n];
}
}
不难发现,我们转移 f[i] 时只依赖 f[i-1] 和 f[i-2] 两个状态。
因此我们可以采用与「滚动数组」类似的思路,只创建长度为 3 的数组,通过取余的方式来复用不再需要的下标。
class Solution {
public int numDecodings(String s) {
int n = s.length();
s = " " + s;
char[] cs = s.toCharArray();
int[] f = new int[3];
f[0] = 1;
for (int i = 1; i <= n; i++) {
f[i % 3] = 0;
int a = cs[i] - '0', b = (cs[i - 1] - '0') * 10 + (cs[i] - '0');
if (1 <= a && a <= 9) f[i % 3] = f[(i - 1) % 3];
if (10 <= b && b <= 26) f[i % 3] += f[(i - 2) % 3];
}
return f[n % 3];
}
}
#94. 二叉树的中序遍历
- Medium
- 2020.10.01:😭
- 2021.07.15:😎
题目:
给定一个二叉树的根节点 root ,返回它的 中序 遍历。
分析:
方法一:递归
方法二:迭代实现(使用栈) 主要思想:先遍历左子树,再取根节点的值,再遍历右子树
- 步骤一:遍历左子树
- 步骤二:取根节点的值
- 步骤三:遍历右子树
代码:
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
while(root!=null||(!stack.empty())){
if(root!=null){
stack.push(root);//把根节点放入栈中
root=root.left;//步骤一,遍历左子树
}else{
TreeNode tem=stack.pop();
list.add(tem.val);//步骤二,取根结点的值
root=tem.right;//步骤三,遍历右子树
}
}
return list;
}
#101. 对称二叉树
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#103. 二叉树的锯齿形层序遍历
- 中等
- 2020.12.02:😭
题目:
分析:
方法一: 广度优先 + 队列反转
方法二: 双端队列
代码:
// BFS + reverse list
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if (root != null) {
queue.offer(root);
}
List<Integer> list ;
while (!queue.isEmpty()) {
int size = queue.size(); //当前层,元素的数量
list = new ArrayList<>();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll(); //按顺序弹出队列元素,加入集合
list.add(node.val);
if (node.left != null) {
queue.offer(node.left); //当前元素的左子树入队,即把下一层的元素加入队列
}
if (node.right != null) {
queue.offer(node.right); //当前元素的右子树入队,即把下一层的元素加入队列
}
}
if (res.size() % 2 == 1) { //本题中奇数层要翻转下
Collections.reverse(list);
}
res.add(list);
}
return res;
}
// 双端队列
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> ans = new LinkedList<List<Integer>>();
if (root == null) {
return ans;
}
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
nodeQueue.offer(root);
boolean isOrderLeft = true;
while (!nodeQueue.isEmpty()) {
Deque<Integer> levelList = new LinkedList<Integer>();
int size = nodeQueue.size();
for (int i = 0; i < size; i++) {
TreeNode curNode = nodeQueue.poll();
if (isOrderLeft) {
levelList.offerLast(curNode.val);
} else {
levelList.offerFirst(curNode.val);
}
if (curNode.left != null) {
nodeQueue.offer(curNode.left);
}
if (curNode.right != null) {
nodeQueue.offer(curNode.right);
}
}
ans.add(new LinkedList<Integer>(levelList));
isOrderLeft = !isOrderLeft;
}
return ans;
}
#104. 二叉树的最大深度
- easy
- 2020.08.28:😭
- 2020.10.10: 😎(递归)
题目:
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
分析:
方法一:递归 ⭐️
如果我们知道了左子树和右子树的最大深度 l 和 r,那么该二叉树的最大深度即为. $max(l,r)+1$
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们在计算当前二叉树的最大深度时,可以先递归计算出其左子树和右子树的最大深度,然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。
- 时间复杂度:O(n),其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。
- 空间复杂度:O(height),其中height 表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
方法二:广度优先搜索
我们也可以用「广度优先搜索」的方法来解决这道题目,但我们需要对其进行一些修改,此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候,不同于广度优先搜索的每次只从队列里拿出一个节点,我们需要将队列里的所有节点都拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,即我们是一层一层地进行拓展,最后我们用一个变量 ans 来维护拓展的次数,该二叉树的最大深度即为 ans。
- 时间复杂度:O(n)
- 空间复杂度:此方法空间的消耗取决于队列存储的元素数量,其在最坏情况下会达到O(n)
代码:
// ⭐️方法一 递归/深度优先
class Solution {
public int maxDepth(TreeNode root) {
// 因此我们在计算当前二叉树的最大深度时,
// 可以先递归计算出其左子树和右子树的最大深度,然后在 O(1) 时间内计算出当前二叉树的最大深度
if (root == null) return 0;
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
}
// 方法二 广度优先搜索
class Solution {
public int maxDepth(TreeNode root) {
if (root==null ) return 0;
// 队列里存放的是「当前层的所有节点」
Queue<TreeNode> queue = new LinkedList<TreeNode>();
/**
* add是list的
* offer是queue的
* api里说:
* add:Inserts the specified element at the specified position in this list
* 将指定的元素插入到list中指定的的位置。
* offer:
* 如果在不违反容量限制的情况下,尽可能快的将指定的元素插入到queue中去
* */
queue.offer(root);
int ans = 0;
while (!queue.isEmpty()) {
// 每层节点的数量
int size = queue.size();
// 每次拓展下一层的时候,不同于广度优先搜索的每次只从队列里拿出一个节点,我们需要将队列里的所有节点都拿出来进行拓展
for (int i = 0; i < size; i++) {
// poll() 检索并删除此列表的头部(第一个元素)。
TreeNode node = queue.poll();
if (node.left!=null) queue.offer(node.left);
if (node.right!=null) queue.offer(node.right);
}
ans++;
}
return ans;
}
}
#105. 从前序与中序遍历序列构造二叉树
- Medium
- 2020.10.01:😭
- 2020.11.01:😎
题目:
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
分析:
我们肯定要想办法确定根节点的值,把根节点做出来,然后递归构造左右子树即可。
我们先来回顾一下,前序遍历和中序遍历的结果有什么特点?
void traverse(TreeNode root) {
// 前序遍历
preorder.add(root.val);
traverse(root.left);
traverse(root.right);
}
void traverse(TreeNode root) {
traverse(root.left);
// 中序遍历
inorder.add(root.val);
traverse(root.right);
}
这样的遍历顺序差异,导致了preorder和inorder数组中的元素分布有如下特点:
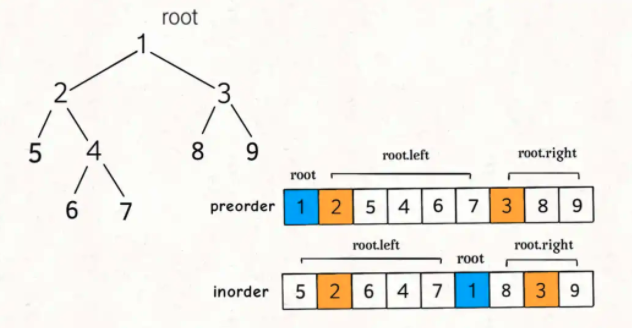
找到根节点是很简单的,前序遍历的第一个值preorder[0]就是根节点的值,关键在于如何通过根节点的值,将preorder和postorder数组划分成两半,构造根节点的左右子树?
换句话说,对于以下代码中的?部分应该填入什么:
/* 主函数 */
TreeNode buildTree(int[] preorder, int[] inorder) {
return build(preorder, 0, preorder.length - 1,
inorder, 0, inorder.length - 1);
}
/*
若前序遍历数组为 preorder[preStart..preEnd],
后续遍历数组为 postorder[postStart..postEnd],
构造二叉树,返回该二叉树的根节点
*/
TreeNode build(int[] preorder, int preStart, int preEnd,
int[] inorder, int inStart, int inEnd) {
// root 节点对应的值就是前序遍历数组的第一个元素
int rootVal = preorder[preStart];
// rootVal 在中序遍历数组中的索引
int index = 0;
for (int i = inStart; i <= inEnd; i++) {
if (inorder[i] == rootVal) {
index = i;
break;
}
}
TreeNode root = new TreeNode(rootVal);
// 递归构造左右子树
root.left = build(preorder, ?, ?,
inorder, ?, ?);
root.right = build(preorder, ?, ?,
inorder, ?, ?);
return root;
}
对于代码中的rootVal和index变量,就是下图这种情况:
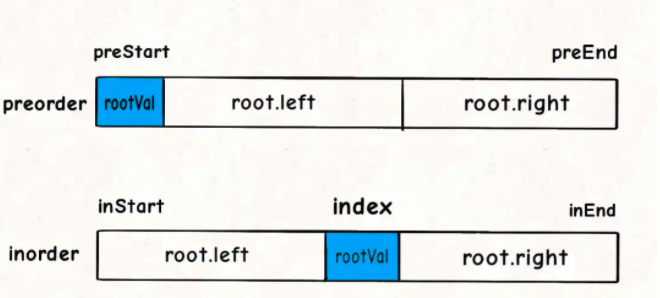
现在我们来看图做填空题,下面这几个问号处应该填什么:
root.left = build(preorder, ?, ?,
inorder, ?, ?);
root.right = build(preorder, ?, ?,
inorder, ?, ?);
对于左右子树对应的inorder数组的起始索引和终止索引比较容易确定:
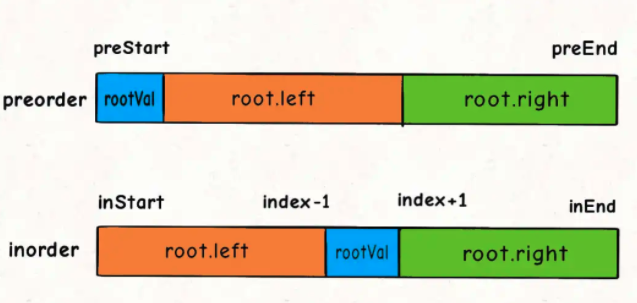
root.left = build(preorder, ?, ?,
inorder, inStart, index - 1);
root.right = build(preorder, ?, ?,
inorder, index + 1, inEnd);
对于preorder数组呢?如何确定左右数组对应的起始索引和终止索引?
这个可以通过左子树的节点数推导出来,假设左子树的节点数为leftSize,那么preorder数组上的索引情况是这样的:
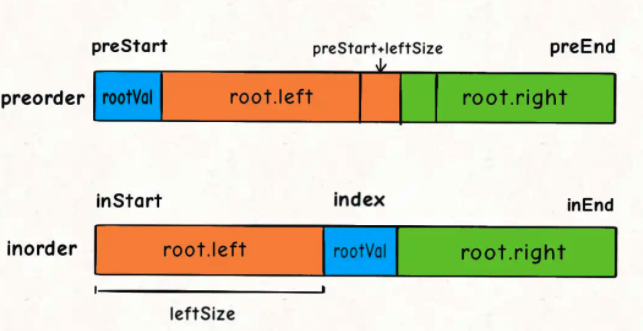
看着这个图就可以把preorder对应的索引写进去了:
int leftSize = index - inStart;
root.left = build(preorder, preStart + 1, preStart + leftSize,
inorder, inStart, index - 1);
root.right = build(preorder, preStart + leftSize + 1, preEnd,
inorder, index + 1, inEnd);
至此,整个算法思路就完成了,我们再补一补 base case 即可写出解法代码:
代码:
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return build(preorder,0,preorder.length-1,
inorder,0,inorder.length-1);
}
// 若前序遍历数组为 preorder[preStart..preEnd],
// 中序遍历数组为 inorder[inStart..inEnd],
// 构造二叉树,返回该二叉树的根节点
public TreeNode build(int[] preorder,int preStart,int preEnd,int[] inorder,int inStart,int inEnd){
// 递归出口
if (preStart>preEnd){
return null;
}
// 先构建根节点 再递归生成左右子树
// root 节点对应的值就是前序遍历数组的第一个元素
int rootVal = preorder[preStart];
// rootVal 再中序数组中的索引
int index = 0;
for (int i = inStart; i <= inEnd ; i++) {
if (inorder[i]==rootVal){
index=i;
break;
}
}
TreeNode root = new TreeNode(rootVal);
// 递归构造左右子树
int leftSize = index-inStart;
root.left = build(preorder,preStart+1,preStart+leftSize,inorder,inStart,index-1);
root.right = build(preorder,preStart+leftSize+1,preEnd,inorder,index+1,inEnd);
return root;
}
}
#106. 从中序与后序遍历序列构造二叉树
- Medium
- 2020.10.01:😎
题目:
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
分析:
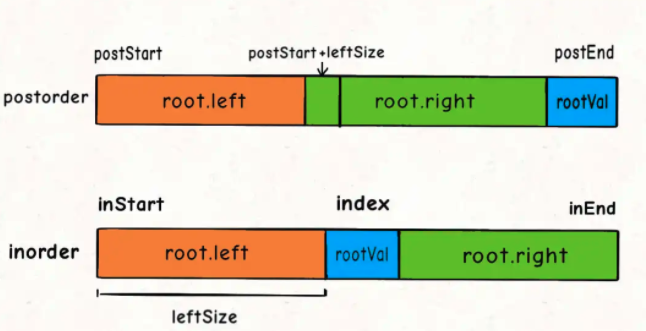
与105类似,现在postoder和inorder对应的状态如下:
- 时间复杂度:O()
- 空间复杂度:O()
代码:
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return build(inorder,0,inorder.length-1,
postorder,0,postorder.length-1);
}
public TreeNode build(int[] inorder,int inStart,int inEnd, int[] postorder,int postStart,int postEnd){
// 递归出口
if (inStart>inEnd) return null;
// 找到根节点
int rootVal = postorder[postEnd]; // 别用postorder.length-1 太浪费时间
int index = -1;
for (int i = inStart; i <=inEnd; i++) {
if (inorder[i]==rootVal) {
index = i;
break;
}
}
// 迭代生成左右子树
TreeNode root = new TreeNode(rootVal);
int leftSize = index-inStart; // 左子树节点个数
root.left = build(inorder,inStart,index-1,postorder,postStart,postStart+leftSize-1);
root.right = build(inorder,index+1,inEnd,postorder,postStart+leftSize,postEnd-1);
return root;
}
}
#108. 将有序数组转换为二叉搜索树
- Medium
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#109. 有序链表转换二叉搜索树
- Medium
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#110. 平衡二叉树
- easy
- 2020.08.28:😭
- 2020.10.14:😎
题目:
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
分析:
方法一:从底至顶(提前阻断),返现不对劲马上返回-1. ⭐️
此方法为本题的最优解法,但“从底至顶”的思路不易第一时间想到。
思路是对二叉树做先序遍历,从底至顶返回子树最大高度,若判定某子树不是平衡树则 “剪枝” ,直接向上返回。
算法流程:
recur(root):
- 递归返回值:
- 当节点
root左 / 右子树的高度差 <=1 :则返回以节点root为根节点的子树的最大高度,即节点root的左右子树中最大高度加 1 (max(left, right) + 1); - 当节点
root左 / 右子树的高度差≥2:则返回 −1 ,代表 此子树不是平衡树 。
- 当节点
- 递归终止条件:
- 当越过叶子节点时,返回高度 0 ;
- 当左(右)子树高度
left== -1时,代表此子树的 左(右)子树 不是平衡树,因此直接返回 −1 ;
isBalanced(root) :
返回值: 若 recur(root) != -1 ,则说明此树平衡,返回 true ; 否则返回 false
复杂度分析: 时间复杂度 O(N): N 为树的节点数;最差情况下,需要递归遍历树的所有节点。 空间复杂度 O(N): 最差情况下(树退化为链表时),系统递归需要使用 O(N) 的栈空间。
方法二:从顶至底(暴力法):
此方法容易想到,但会产生大量重复计算,时间复杂度较高。
构造一个获取当前节点最大深度的方法 depth(root) ,通过比较此子树的左右子树的最大高度差abs(depth(root.left) - depth(root.right)),来判断此子树是否是二叉平衡树。若树的所有子树都平衡时,此树才平衡。
算法流程: isBalanced(root) :判断树 root 是否平衡
- 特例处理: 若树根节点 root 为空,则直接返回 true ;
- 返回值: 所有子树都需要满足平衡树性质,因此以下三者使用与逻辑 && 连接;
- abs(self.depth(root.left) - self.depth(root.right)) <= 1 :判断 当前子树 是否是平衡树;
- self.isBalanced(root.left) : 先序遍历递归,判断 当前子树的左子树 是否是平衡树;
- self.isBalanced(root.right) : 先序遍历递归,判断 当前子树的右子树 是否是平衡树;
depth(root) : 计算树 root 的最大高度
- 终止条件: 当 root 为空,即越过叶子节点,则返回高度 0 ;
- 返回值: 返回左 / 右子树的最大高度加 1 。
复杂度分析: 时间复杂度 O(Nlog2N): 最差情况下, isBalanced(root) 遍历树所有节点,占用 O(N) ;判断每个节点的最大高度 depth(root) 需要遍历 各子树的所有节点 ,子树的节点数的复杂度为 O(log 2N) 空间复杂度O(N): 最差情况下(树退化为链表时),系统递归需要使用 O(N) 的栈空间。
代码:
// ⭐️ 方法一
// 对二叉树做先序遍历,从底至顶返回子树最大高度,若判定某子树不是平衡树则 “剪枝” ,直接向上返回
public boolean isBalanced(TreeNode root) {
return recur(root) != -1;
}
private int recur(TreeNode root) {
if (root == null) return 0;
int left = recur(root.left);
// 当左(右)子树高度 left== -1 时,代表此子树的 左(右)子树 不是平衡树,因此直接返回 -1 ;
if(left == -1) return -1;
int right = recur(root.right);
if(right == -1) return -1;
// 当 左/右 子树深度差大于 1 时,返回 -1 ;否则,返回 左/右子树深度最大值 + 1
// max(left, right) + 1 为当前子树的深度;以此作为返回值,才能判断树是否是"平衡二叉树",即 abs(left - right) <=1 是否成立
return Math.abs(left - right) <=1 ? Math.max(left, right) + 1 : -1;
}
// 方法二
public boolean isBalanced(TreeNode root) {
if(root==null) return true;
// 比较此子树的左右子树的最大高度差
return (Math.abs(depth(root.left)-depth(root.right))<=1)
&& isBalanced(root.left)
&& isBalanced(root.right);
}
// 获取当前节点最大深度
// 终止条件: 当 root 为空,即越过叶子节点,则返回高度 0
private int depth(TreeNode root){
if (root ==null) return 0;
return Math.max(depth(root.left),depth(root.right))+1;
}
#111. 二叉树的最小深度
- easy
- 2020.10.01:😭
题目:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例:
输入:root = [3,9,20,null,null,15,7]
输出:2
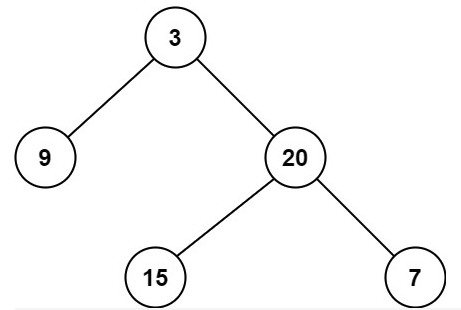
分析:
方法一:BFS
怎么套到 BFS 的框架里呢?首先明确一下起点 start 和终点 target 是什么,怎么判断到达了终点?
显然起点就是 root 根节点,终点就是最靠近根节点的那个「叶子节点」嘛,叶子节点就是两个子节点都是 null 的节点:
if (cur.left == null && cur.right == null)
// 到达叶子节点
那么,按照我们上述的框架稍加改造来写解法即可:
public int minDepth(TreeNode root) {
if (root == null) return 0;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offer(root);
// root 本身就是一层,depth 初始化为1
int depth = 1;
while (!queue.isEmpty()) {
int size = queue.size();
// 将当前队列中的所有节点向四周扩散
for (int i = 0; i < size; i++) {
TreeNode cur = queue.poll(); // poll() 检索并删除此列表的头部(第一个元素)
// 判断是否达到终点
if (cur.left == null && cur.right == null) return depth;
if (cur.left != null) queue.offer(cur.left);
if (cur.right != null) queue.offer(cur.right);
}
// 增加步数
depth++;
}
return depth;
}
二叉树是很简单的数据结构,我想上述代码你应该可以理解的吧,其实其他复杂问题都是这个框架的变形,再探讨复杂问题之前,我们解答两个问题:
1、为什么 BFS 可以找到最短距离,DFS 不行吗?
首先,你看 BFS 的逻辑,depth 每增加一次,队列中的所有节点都向前迈一步,这保证了第一次到达终点的时候,走的步数是最少的。
DFS 不能找最短路径吗?其实也是可以的,但是时间复杂度相对高很多。你想啊,DFS 实际上是靠递归的堆栈记录走过的路径,你要找到最短路径,肯定得把二叉树中所有树杈都探索完才能对比出最短的路径有多长对不对?而 BFS 借助队列做到一次一步「齐头并进」,是可以在不遍历完整棵树的条件下找到最短距离的。
形象点说,DFS 是线,BFS 是面;DFS 是单打独斗,BFS 是集体行动。这个应该比较容易理解吧。
2、既然 BFS 那么好,为啥 DFS 还要存在?
BFS 可以找到最短距离,但是空间复杂度高,而 DFS 的空间复杂度较低。
还是拿刚才我们处理二叉树问题的例子,假设给你的这个二叉树是满二叉树,节点数为 N,对于 DFS 算法来说,空间复杂度无非就是递归堆栈,最坏情况下顶多就是树的高度,也就是 O(logN)。
但是你想想 BFS 算法,队列中每次都会储存着二叉树一层的节点,这样的话最坏情况下空间复杂度应该是树的最底层节点的数量,也就是 N/2,用 Big O 表示的话也就是 O(N)。
由此观之,BFS 还是有代价的,一般来说在找最短路径的时候使用 BFS,其他时候还是 DFS 使用得多一些(主要是递归代码好写)。
#112. 路径总和
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#114. 二叉树展开为链表
- 中等
- 2020.10.01:😭
- 2020.10.27:😭 while写成了if
- 2020.11.01:😭 忘记把左子树置空了,只差一点点距离!
题目:
给定一个二叉树,原地将它展开为一个单链表。
例如,给定二叉树
1
/ \
2 5
/ \ \
3 4 6
将其展开为:
1
\
2
\
3
\
4
\
5
\
6
分析:
我们尝试给出这个函数的定义:
给flatten函数输入一个节点root,那么以root为根的二叉树就会被拉平为一条链表。
我们再梳理一下,如何按题目要求把一棵树拉平成一条链表?很简单,以下流程:
1、将左子树作为右子树
2、将原先的右子树接到当前右子树的末端
上面三步看起来最难的应该是第一步对吧,如何把root的左右子树拉平?其实很简单,按照flatten函数的定义,对root的左右子树递归调用flatten函数即可:
⚠️:另外注意递归框架是后序遍历,因为我们要先拉平左右子树才能进行后续操作。
代码:
public void flatten(TreeNode root) {
// base case
if (root == null) return;
flatten(root.left);
flatten(root.right);
/**** 后序遍历位置 ****/
// 1、将左子树作为右子树,并把左子树置空
TreeNode temp = root.right;
root.right = root.left;
root.left = null;
// 2、将原先的右子树接到当前右子树的末端
while (root.right != null) { // ⚠️ while非常重要,需要循环找到最后当前右子树的末端
root = root.right;
}
root.right = temp;
}
#116. 填充每个节点的下一个右侧节点指针
- 中等
- 2020.10.01:😭
- 2020.10.27:😭 无法处理跨父节点连接
- 2020.11.01:😭 奇怪的前序遍历
题目:
给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
提示:
你只能使用常量级额外空间。
使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
分析:
题目的意思就是把二叉树的每一层节点都用next指针连接起来:
而且题目说了,输入是一棵「完美二叉树」,形象地说整棵二叉树是一个正三角形,除了最右侧的节点next指针会指向null,其他节点的右侧一定有相邻的节点。
⚠️ 二叉树的问题难点在于,如何把题目的要求细化成每个节点需要做的事情,但是如果只依赖一个节点的话,肯定是没办法连接「跨父节点」的两个相邻节点的。
那么,我们的做法就是增加函数参数,一个节点做不到,我们就给他安排两个节点,「将每一层二叉树节点连接起来」可以细化成「将每两个相邻节点都连接起来」:
这样,connectTwoNode函数不断递归,可以无死角覆盖整棵二叉树,将所有相邻节点都连接起来,也就避免了我们之前出现的问题,这道题就解决了。
代码:
class Solution {
public Node connect(Node root) {
if (root == null) return null;
connectTwoNode(root.left, root.right);
return root;
}
// 定义:输入两个节点,将它俩连接起来
public void connectTwoNode(Node node1, Node node2) {
if (node1 == null || node2 == null) {
return;
}
/**** 前序遍历位置 ****/
// 将传入的两个节点连接
node1.next = node2;
// 连接相同父节点的两个子节点
connectTwoNode(node1.left, node1.right);
connectTwoNode(node2.left, node2.right);
// 连接跨越父节点的两个子节点
connectTwoNode(node1.right, node2.left);
}
}
#141. 判断链表是否存在环
- Easy
- 2019.09.13:😭
- 2021.03.05: 😎
题目:
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
实例1:
分析:
方法一:哈希表
我们遍历所有结点并在哈希表中存储每个结点的引用(或内存地址)。如果当前结点为空结点 null(即已检测到链表尾部的下一个结点),那么我们已经遍历完整个链表,并且该链表不是环形链表。如果当前结点的引用已经存在于哈希表中,那么返回 true(即该链表为环形链表)。
复杂度分析:
时间复杂度:O(n),对于含有 n 个元素的链表,我们访问每个元素最多一次。添加一个结点到哈希表中只需要花费 O(1)的时间。
空间复杂度:O(n),空间取决于添加到哈希表中的元素数目,最多可以添加 n 个元素。
方法二:双指针 ⭐️
通过使用具有 不同速度 的快、慢两个指针遍历链表,空间复杂度可以被降低至 O(1)。慢指针每次移动一步,而快指针每次移动两步。
如果列表中不存在环,最终快指针将会最先到达尾部,此时我们可以返回 false。
现在考虑一个环形链表,把慢指针和快指针想象成两个在环形赛道上跑步的运动员(分别称之为慢跑者与快跑者)。而快跑者最终一定会追上慢跑者。这是为什么呢?考虑下面这种情况(记作情况 A)- 假如快跑者只落后慢跑者一步,在下一次迭代中,它们就会分别跑了一步或两步并相遇。
其他情况又会怎样呢?例如,我们没有考虑快跑者在慢跑者之后两步或三步的情况。但其实不难想到,因为在下一次或者下下次迭代后,又会变成上面提到的情况 A。
代码:
// 方法一
public class Solution {
public boolean hasCycle(ListNode head) {
HashSet<ListNode> set = new HashSet<>();
while(head!=null){
if(set.contains(head)){
return true;
}
set.add(head);
head=head.next;
}
return false;
}
}
// 方法二 ⭐️
public boolean hasCycle(ListNode head) {
if(head == null) return false;
ListNode fast = head;
ListNode slow = head;
while(fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
if(fast == slow){
return true;
}
}
return false;
}
#142. 环形链表 II
- 中等
- 2021.04.08:😭
题目:
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
说明:不允许修改给定的链表。使用 O(1) 空间解决此题.
分析:
方法一: 快慢指针 + 数学
根据:
-
设链表共有 a+b个节点,其中 链表头部到链表入口 有 a 个节点(不计链表入口节点), 链表环 有 b 个节点。f快指针走过的步数,s慢指针走过的步数。
- f=2s (快指针每次2步,路程刚好2倍)
- f = s + nb (相遇时,刚好多走了n圈)
推出:s = nb
从head结点走到入环点需要走 : a + nb, 而slow已经走了nb,那么slow再走a步就是入环点了。
如何知道slow刚好走了a步? 从head开始,和slow指针一起走,相遇时刚好就是a步
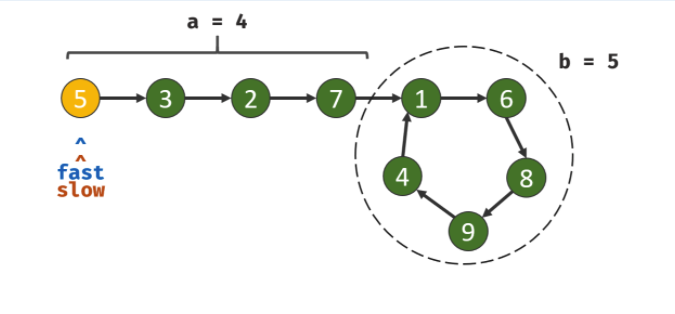
要是想求环的长度怎么办呢 继续一快一慢,维护一个count=1;循环直第二次相遇,每次循环count++。
代码:
public ListNode detectCycle(ListNode head) {
if(head==null||head.next==null) return null;
ListNode slow = head;
ListNode fast = head;
while(fast.next!=null&&fast.next.next!=null){
slow = slow.next;
fast = fast.next.next;
if(slow==fast){
fast = head;
while(fast!=slow){
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
return null;
}
// 要是想求环的长度怎么办呢 继续一快一慢,维护一个count=1;循环直第二次相遇,每次循环count++。
public int hasCycleLength(ListNode head) {
if (head==null||head.next==null) return -1;
ListNode quick = head;
ListNode slow = head;
while (true){
if(quick==null||quick.next==null) return -1;
quick = quick.next.next;
slow = slow.next;
if (quick==slow) break;
}
int count = 1;
quick = quick.next;
while (slow!=quick){
slow = slow.next;
quick = quick.next;
count++;
}
return count;
}
143. 重排链表
- 中等
- 2021.11.22:
题目:
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
分析:
方法一:线性表
因为链表不支持下标访问,所以我们无法随机访问链表中任意位置的元素。
因此比较容易想到的一个方法是,我们利用线性表存储该链表,然后利用线性表可以下标访问的特点,直接按顺序访问指定元素,重建该链表即可。
方法二:寻找链表中点 + 链表逆序 + 合并链表
目标链表即为将原链表的左半端和反转后的右半端合并后的结果,因此该任务可以划分为三步:
- 找到原链表的中点(快慢指针) - #876
- 将原链表的右半端反转(反转链表) - #206
- 将原链表的两端合并,因为两链表长度相差不超过 1,因此直接合并即可。- #21
代码:
// 方法一:线性表
public void reorderList(ListNode head) {
if (head == null) {
return;
}
List<ListNode> list = new ArrayList<ListNode>();
ListNode node = head;
while (node != null) {
list.add(node);
node = node.next;
}
int i = 0, j = list.size() - 1;
while (i < j) {
list.get(i).next = list.get(j);
i++;
list.get(j).next = list.get(i);
j--;
}
list.get(i).next = null;
}
// 方法二:寻找链表中点 + 链表逆序 + 合并链表
public void reorderList(ListNode head) {
// 快慢指针找中点
ListNode quick = head;
ListNode slow = head;
while(quick.next!=null&&quick.next.next!=null){
slow = slow.next;
quick = quick.next.next;
}
ListNode head2 = slow.next;
slow.next = null; // 断开链表
// 反转后链表头节点为pre指针
ListNode pre = null;
ListNode cur = head2;
while(cur!=null){
ListNode temp = cur.next;
cur.next = pre;
pre = cur;
cur = temp;
}
// 合并链表
mergeList(head,pre);
}
public void mergeList(ListNode head1, ListNode head2) {
while(head1!=null && head2!=null){
ListNode temp1 = head1.next;
ListNode temp2 = head2.next;
head1.next = head2;
head2.next = temp1;
head1 = temp1;
head2 = temp2;
}
// #21-跟通用的合并链表(返回合并后的头节点)
public ListNode mergeList2(ListNode head1, ListNode head2) {
// 哨兵节点
ListNode dummyHead = new ListNode(-1);
ListNode pre = dummyHead;
while(head1!=null&&head2!=null){
pre.next = head1;
head1 = head1.next;
pre = pre.next;
pre.next = head2;
head2 = head2.next;
pre = pre.next;
}
pre.next = head1==null?head2:head1;
return dummyHead.next;
}
}
#144. 二叉树的前序遍历
- Medium
- 2020.10.01:😭
- 2021.07.15:😎
题目:
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
分析:
方法一:递归
方法二:迭代实现(使用栈)
先取根节点的值,再遍历左子树,再遍历右子树。步骤:
- 步骤一:取根节点的值
- 步骤二:遍历左子树
- 步骤三:遍历右子树
本质上是在模拟递归,因为在递归的过程中使用了系统栈,所以在迭代的解法中常用Stack来模拟系统栈。
首先我们应该创建一个Stack用来存放节点,首先我们想要打印根节点的数据,此时Stack里面的内容为空,所以我们优先将头结点加入Stack,然后打印。
之后我们应该先打印左子树,然后右子树。所以在root加入stack后先将其替换为左子树root=root.left。
如果左子树不存在则弹出root替换为其右子树。
此时你能得到的流程如下:
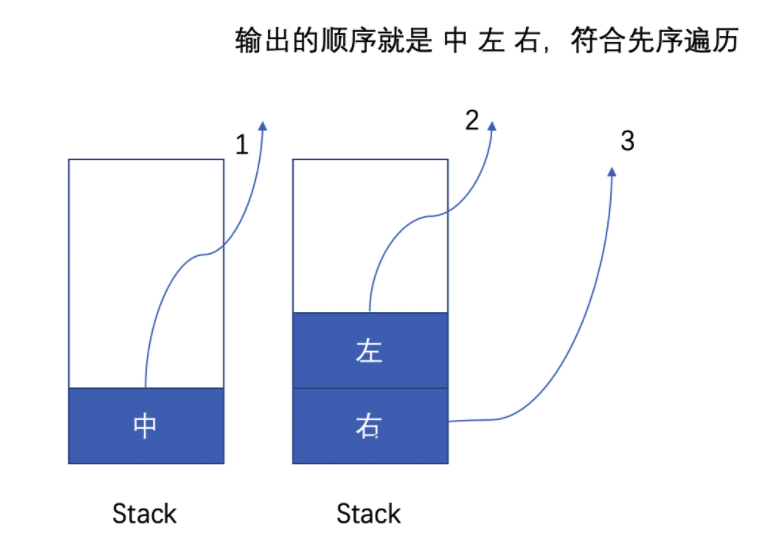
代码:
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
while(root!=null||(!stack.isEmpty())){
if(root!=null){
stack.push(root);//步骤一,把根节点放入栈中,同时打印该节点(本题中为放入list)
list.add(root.val);
root=root.left;//步骤二,遍历左子树
}else{
root=stack.pop().right;//步骤三,遍历右子树
}
}
return list;
}
#145. 二叉树的后序遍历
- Medium
- 2020.10.01:😭
- 2021.07.15:😎
题目:
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
分析:
方法一:递归
方法二:迭代实现(使用栈) 后序遍历,可以看成将一颗树左右反转,然后先序遍历,左后的结果取反。
后续遍历 = reverse(反转树先序遍历)
我们也可以用迭代的方式实现方法一的递归函数,两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其余的实现与细节都相同,具体可以参考下面的代码。
主要思想:先遍历左子树,再遍历右子树,最后取根节点的值。步骤:(对主要思想里边的步骤逆序处理 左右根–>根右左 )
- 步骤一:取根节点的值,插入list最后边
- 步骤二:遍历右子树
- 步骤三:遍历左子树
代码:
// 递归实现
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
postorder(root, res);
return res;
}
public void postorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val);
}
// 迭代实现 后序遍历,可以看成将一颗树左右反转,然后先序遍历,左后的结果取反。
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
while(root!=null||(!stack.isEmpty())){
if(root!=null){
stack.push(root);//把根节点放入栈中
list.add(0,root.val);//步骤一,在index=0处插入根结点的值
root=root.right;//步骤二,遍历右子树
}else{
root=stack.pop().left;//步骤三,遍历左子树
}
}
return list;
}
#146. LRU 缓存机制
- Medium
- 2020.10.01:😭
题目:
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制 。
实现 LRUCache 类:
LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶:你是否可以在 O(1) 时间复杂度内完成这两种操作?
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
分析:
方法一:LinkedHashMap JDK实现
方法二:HashMap + 自己实现双向链表
-
在双向链表的实现中,使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限,这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。

- 时间复杂度:O(1)
- 空间复杂度:O(1)
代码:
// 方法二 HashMap + 自己实现双向链表
class LRUCache {
private HashMap<Integer,DLinkedListNode> cache = new HashMap<>();
private DLinkedListNode dummyHead= new DLinkedListNode(); // 伪头部
private DLinkedListNode dummyTail= new DLinkedListNode(); // 伪尾部
private int size; // 链表当前当长度(排除伪节点)
private int capacity; // LRU容量
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
// 初始化伪节点引用
this.dummyHead.next = this.dummyTail;
this.dummyTail.prev = this.dummyHead;
}
public int get(int key) {
DLinkedListNode node = cache.get(key);
if (node==null){
return -1;
}
// 如果缓存存在,将它移动到链表头部
moveToHead(node);
return node.value;
}
// 插入逻辑
public void put(int key, int value) {
// 如果存在就通过cache快速找到node,更新值后移动到链表的头部
DLinkedListNode node = this.cache.get(key);
if (node!=null){
node.value = value;
moveToHead(node);
}else {
// 不存在则创建节点放入链表的头部并放入cache,然后判断列表容量是否已满,满了的话需要删除链表中的尾节点和cache
node = new DLinkedListNode(key,value);
cache.put(key,node);
size++;
// 插入头部
addToHead(node);
if (size>capacity){
// 删除链表中的尾节点和cache
DLinkedListNode tailNode = this.dummyTail.prev;
removeNode(tailNode);
this.cache.remove(tailNode.key);
size--;
}
}
}
// 将该节点移动到头部
private void moveToHead(DLinkedListNode node) {
// 先删除该节点 让它的前驱节点指向后继节点
removeNode(node);
// 将该节点插入到伪头部之后
addToHead(node);
}
private void addToHead(DLinkedListNode node) {
node.prev = this.dummyHead;
node.next = this.dummyHead.next;
this.dummyHead.next.prev = node;
this.dummyHead.next = node;
}
private void removeNode(DLinkedListNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
class DLinkedListNode {
int key;
int value;
DLinkedListNode prev;
DLinkedListNode next;
public DLinkedListNode() {
}
public DLinkedListNode(int key, int value) {
this.key = key;
this.value = value;
}
}
}
#152. 乘积最大子数组
- 中等
- 2022.03.07:
题目:
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
分析:
方法一:动态规划
这题是求数组中子区间的最大乘积,对于乘法,我们需要注意,负数乘以负数,会变成正数,所以解这题的 时候我们需要维护两个变量,当前的最大值,以及最小值,最小值可能为负数,但没准下一步乘以一个负 数,当前的最大值就变成最小值,而最小值则变成最大值了。
我们的动态方程可能这样:
-
maxDP[i] = max(nums[i], maxDP[i-1]*nums[i], minDP[i-1]*nums[i]) -
minDP[i] = min(nums[i], minDP[i-1]*nums[i], maxDP[i-1]*nums[i]) -
dp[i] = max(dp[i-1], maxDP[i])
其中,与i元素自己进行比较是为了处理i元素之前全都是0的情况。如果nums[i]为0,那么maxDP和minDP都为0, 我们需要从nums[i+1]重新开始。
方法二:一次遍历,保存阶段最大值/阶段最小值
- 遍历数组时计算结果最大值max,不断更新
- 令curMax为阶段最大值,则阶段最大值为
curMax=max(curMax*nums[i],nums[i]) - 由于存在负数,那么会导致最大的变最小的,最小的变最大的。因此还需要维护阶段最小值curMin,
curMin=min(curMin[i],nums[i]) - 因此当负数出现时则curMax与curMin进行交换再进行下一步计算
代码:
// 方法一
public int maxProduct(int[] nums) {
if(nums.length == 0) return 0;
int ans = nums[0];
//两个mDP分别定义为以i结尾的子数组的最大积与最小积;
int[] maxDP = new int[nums.length];
int[] minDP = new int[nums.length];
//初始化DP;
maxDP[0] = nums[0];
minDP[0] = nums[0];
for(int i = 1; i < nums.length; i++){
//最大积的可能情况有:元素i自己本身,上一个最大积与i元素累乘,上一个最小积与i元素累乘;
//与i元素自己进行比较是为了处理i元素之前全都是0的情况;
maxDP[i] = Math.max(nums[i], Math.max(maxDP[i-1]*nums[i], minDP[i-1]*nums[i]));
minDP[i] = Math.min(nums[i], Math.min(maxDP[i-1]*nums[i], minDP[i-1]*nums[i]));
//记录ans;
ans = Math.max(ans, maxDP[i]);
}
return ans;
}
// 方法二
public int maxProduct(int[] nums) {
int max = Integer.MIN_VALUE; //结果最大值
int curMax = 1; //阶段最大值
int curMin = 1; //阶段最小值
for(int i = 0; i<nums.length; i++){
//当遇到负数的时候进行交换,因为阶段最小*负数就变阶段最大了,反之同理
if(nums[i] < 0){
int temp = curMax;
curMax = curMin;
curMin = temp;
}
//在这里用乘积和元素本身比较的意思是:
//对于最小值来说,最小值是本身则说明这个元素值比前面连续子数组的最小值还小。⭐️相当于重置了阶段最小值的起始位置
curMax = Math.max(curMax*nums[i],nums[i]);
curMin = Math.min(curMin*nums[i],nums[i]);
//对比阶段最大值和结果最大值
max = Math.max(max,curMax);
}
return max;
}
#160. 相交链表
- 简单
- 2021.05.26
题目:
编写一个程序,找到两个单链表相交的起始节点。
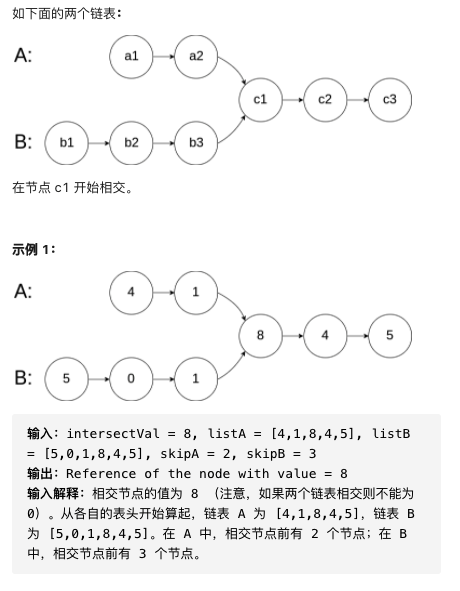
分析:
先判断单链表有没有环,设置两个指针,一个走一步,一个走两步,如果能相遇则说明存在环。#141 判断链表是否存在环
case1:无环场景下(两个都没环)
可以理解成两个人速度一致, 走过的路程一致。那么肯定会同一个时间点到达终点。如果到达终点的最后一段路两人都走的话,那么这段路上俩人肯定是肩并肩手牵手的。
设链表A的长度为a+c,链表B的长度为b+c,a为链表A不公共部分,b为链表B不公共部分,c为链表A、B的公共部分。
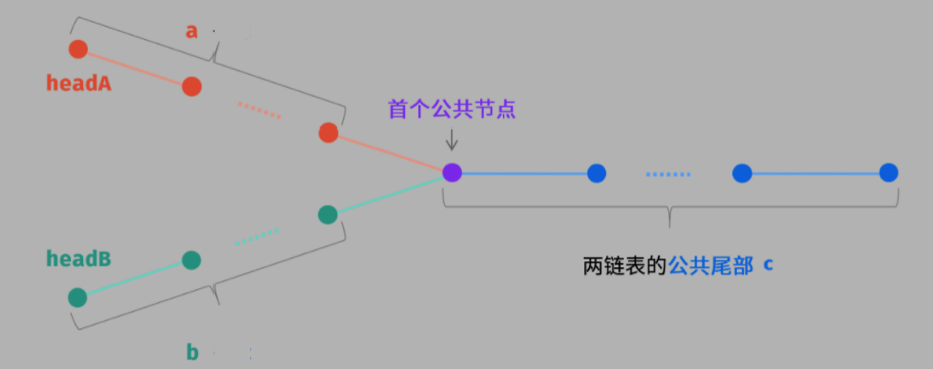
将两个链表连起来,A->B和B->A,长度:a+c+b+c=b+c+a+c:
- 若链表AB相交,则a+c+b与b+c+a就会抵消,它们就会在c处相遇;
- 若不相交,则c为null,则a+b=b+a,它们各自移动到尾部循环结束,即返回null。
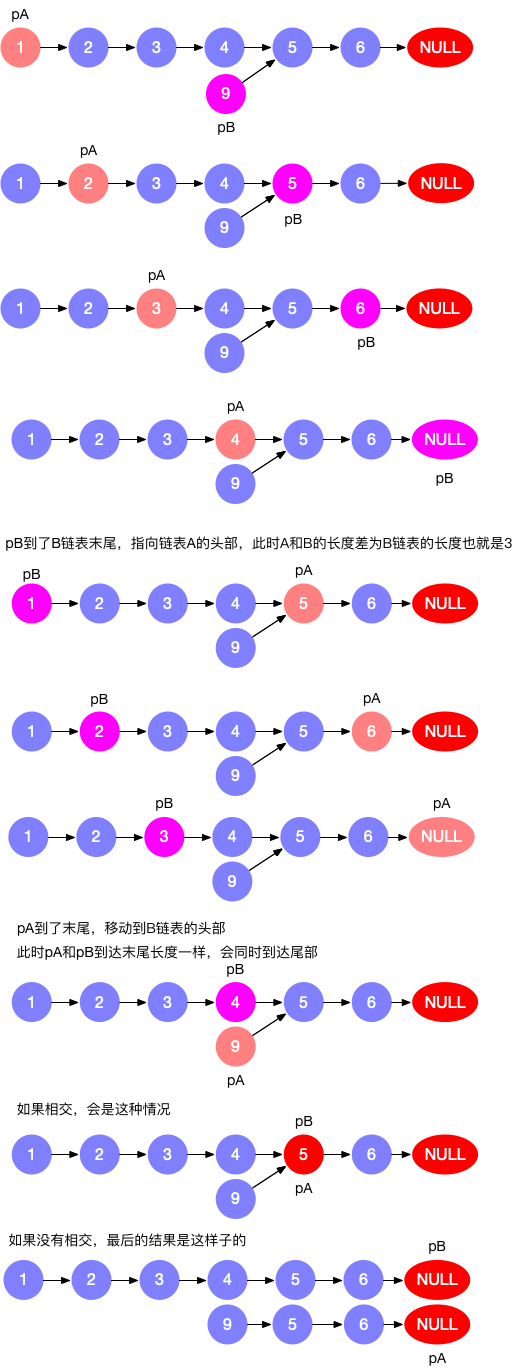
case2:两个都有环,如何判断两链表是否相交
若两个链表都有环,则分别得到每个链表的入环节点node1,node2,然后进行有环单链表判断是否相交。 #142. 环形链表 II
- 第一种:不相交。
- 第二种:环外相交。单链表相交那肯定是同一个环,所以入环节点肯定是同一个,直接返回即可。
- 第三种:环内相交,如果遇到了,那么两个入环节点都是最近的点,任意返回一个都可以。
如果两个环的入环节点相等,就是第二个,不是就是1或3。区分1和3,选一个链表的入环节点开始next遍历,如果在再次遇到这个节点之前没有遇到另一个入环节点就是1,如果相遇了就是3,此时任选一个返回就好了。
case3:一个有环,一个没环:不用判断了,肯定两链表不相交
代码:
// 无环场景下
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode A = headA;
ListNode B = headB;
while (A != B) {
A = A != null ? A.next : headB;
B = B != null ? B.next : headA;
}
return A; // 不相交也会返回null
}
}
// 有环场景下
public static ListNode getIntersectionNode(ListNode headA,ListNode headB){
ListNode cycleNodeA = detectCycle(headA);
ListNode cycleNodeB = detectCycle(headB);
// 如果入环节点相同,则两有环单链表环外相交
if (cycleNodeA==cycleNodeB){
return cycleNodeA;
}
// 环内相交(环内转一圈还没找到CycleB说明两有环单链表不相交)
node = cycleNodeA.next;
while(node != cycleNodeA){
if(node == cycleNodeB){
return cycleNodeA;
}
}
// 两有环单链表不相交
return null;
}
// 返回入环节点-142. 环形链表 II
public ListNode detectCycle(ListNode head) {
if(head==null||head.next==null) return null;
ListNode slow = head;
ListNode fast = head;
while(fast.next!=null&&fast.next.next!=null){
slow = slow.next;
fast = fast.next.next;
if(slow==fast){
fast = head;
while(fast!=slow){
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
return null;
}
#167. 有序数组的 Two Sum
- easy
- 2019.09.15:😭
- 2019.09.16:😎
- 2021.03.05:😎
题目:
给定一个已按照升序排列的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
分析:
方法一:二分查找
在数组中找到两个数,使得它们的和等于目标值,可以首先固定第一个数,然后寻找第二个数,第二个数等于目标值减去第一个数的差。利用数组的有序性质,可以通过二分查找的方法寻找第二个数。为了避免重复寻找,在寻找第二个数时,只在第一个数的右侧寻找。
时间复杂度:O(nlogn),其中 n 是数组的长度。需要遍历数组一次确定第一个数,时间复杂度是 O(n),寻找第二个数使用二分查找,时间复杂度是 O(logn),因此总时间复杂度是 O(nlogn)。
空间复杂度:O(1)
方法二:双指针
初始时两个指针分别指向第一个元素位置和最后一个元素的位置。每次计算两个指针指向的两个元素之和,并和目标值比较。如果两个元素之和等于目标值,则发现了唯一解。如果两个元素之和小于目标值,则将左侧指针右移一位。如果两个元素之和大于目标值,则将右侧指针左移一位。移动指针之后,重复上述操作,直到找到答案。
使用双指针的实质是缩小查找范围。那么会不会把可能的解过滤掉?
如果左指针先到达下标 i 的位置,此时右指针还在下标 j 的右侧,sum>target,因此一定是右指针左移,左指针不可能移到 i 的右侧。
如果右指针先到达下标 j 的位置,此时左指针还在下标 i 的左侧,sum<target,因此一定是左指针右移,右指针不可能移到 j 的左侧。
由此可见,在整个移动过程中,左指针不可能移到 i 的右侧,右指针不可能移到 j 的左侧,因此不会把可能的解过滤掉。由于题目确保有唯一的答案,因此使用双指针一定可以找到答案。
时间复杂度:O(n),其中 n 是数组的长度。两个指针移动的总次数最多为 n 次。
空间复杂度:O(1)
代码:
// 方法一 二分查找
class Solution {
// 可以首先固定第一个数,然后寻找第二个数,第二个数等于目标值减去第一个数的差。
// 利用数组的有序性质,可以通过二分查找的方法寻找第二个数。
public int[] twoSum(int[] numbers, int target) {
for (int i = 0; i < numbers.length; i++) {
int low = i + 1; // 为了避免重复寻找,在寻找第二个数时,只在第一个数的右侧寻找(low=i+1)。
int high = numbers.length - 1;
while (low <= high) {
int mid = (high - low) / 2 + low; // 如果用mid=(left+right)/2,在运行二分查找程序时可能溢出超时。因为如果left和right相加超过int表示的最大范围时就会溢出变为负数。所以如果想避免溢出,不能使用mid=(left+right)/2,应该使用mid=left+(right-left)/2。
if (numbers[mid] == target - numbers[i]) {
return new int[]{i + 1, mid + 1};
} else if (numbers[mid] > target - numbers[i]) {
high = mid - 1; // mid+i > target high指针移到mid左边
} else {
low = mid + 1;
}
}
}
return new int[]{-1, -1};
}
}
// 方法二 双指针
class Solution {
public int[] twoSum(int[] numbers, int target) {
int low = 0, high = numbers.length - 1; // 定义指针
while (low < high) {
int sum = numbers[low] + numbers[high];
if (sum == target) {
return new int[]{low + 1, high + 1};
} else if (sum < target) { // 因为是有序数组
++low; // 小于target的话头指针++
} else {
--high; // 大于target的话尾指针++
}
}
return new int[]{-1, -1};
}
}
#169. 多数元素
- Easy
- 2019.08.30:😭 哈希表,naive!
- 2019.08.30:😎 哈希表
题目:
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
分析:
方法一:哈希表
思路:
遍历整个数组,对记录每个数值出现的次数(利用HashMap,其中key为数值,value为出现次数);
接着遍历HashMap中的每个Entry,寻找value值> nums.length/2 的key即可。
复杂度分析:
时间复杂度:O(n)。
空间复杂度:O(n)。哈希表最多包含 n - [n/2] 个键值对,所以占用的空间为 O(n)。
方法二:排序 众数
思路:
如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序,那么下标为 [n/2] 的元素(下标从 0 开始)一定是众数。
算法:
对于这种算法,我们先将 nums 数组排序,然后返回上文所说的下标对应的元素。下面的图中解释了为什么这种策略是有效的。在下图中,第一个例子是 n 为奇数的情况,第二个例子是 n 为偶数的情况。
对于每种情况,数组下面的线表示如果众数是数组中的最小值时覆盖的下标,数组下面的线表示如果众数是数组中的最大值时覆盖的下标。对于其他的情况,这条线会在这两种极端情况的中间。对于这两种极端情况,它们会在下标为 [n/2] 的地方有重叠。因此,无论众数是多少,返回 [n/2]下标对应的值都是正确的。
复杂度分析:
时间复杂度:O(nlogn)。将数组排序的时间复杂度为 O(nlogn)。
空间复杂度:O(logn)。如果使用语言自带的排序算法,需要使用 O(logn) 的栈空间。如果自己编写堆排序,则只需要使用 O(1) 的额外空间。
方法三:摩尔投票法
摩尔投票法,遇到相同的数,就投一票,遇到不同的数,就减一票,最后还存在票的数就是众数
候选人(cand_num)初始化为nums[0],票数count初始化为1。
当遇到与cand_num相同的数,则票数count = count + 1,否则票数count = count - 1。
当票数count为0时,更换候选人,并将票数count重置为1。
遍历完数组后,cand_num即为最终答案。
为何这行得通呢?
投票法是遇到相同的则票数 + 1,遇到不同的则票数 - 1。
且“多数元素”的个数> ⌊ n/2 ⌋,其余元素的个数总和<= ⌊ n/2 ⌋。
因此“多数元素”的个数 - 其余元素的个数总和 的结果 肯定 >= 1。
这就相当于每个“多数元素”和其他元素 两两相互抵消,抵消到最后肯定还剩余至少1个“多数元素”。
无论数组是1 2 1 2 1,亦或是1 2 2 1 1,总能得到正确的候选人。
方法二说明:

代码:
// 方法一:哈希表计数法 ☑️
class Solution {
public int majorityElement(int[] nums) {
int limit = nums.length/2;
// 1 遍历整个数组放入HashMap key为数值,value为次数
Map<Integer,Integer> map = new HashMap<>(); //构造一个具有指定初始容量和默认负载因子(0.75)的空HashMap。
for (int num : nums) {
map.merge(num,1,(o_val,n_val)->{return o_val+n_val;}); //它将新的值赋值给到key中(如果不存在)或更新具有给定值的现有key(UPSERT)
}
// 2 遍历HashMap中的每个Entry 寻找value大于半数的值
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
if (entry.getValue()>limit) return entry.getKey();
}
return -1
}
}
// 方法二: 排序 ☑️
class Solution {
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length/2];
}
}
// 方法三:摩尔投票法
// 摩尔投票法,遇到相同的数,就投一票,遇到不同的数,就减一票,最后还存在票的数就是众数
class Solution {
public int majorityElement(int[] nums) {
int cand_num = nums[0], count = 1;
for (int i = 1; i < nums.length; ++i) {
if (cand_num == nums[i])
++count;
else if (--count == 0) {
cand_num = nums[i];
count = 1;
}
}
return cand_num;
}
}
205. 同构字符串
- 简单
- 2021.11.27:
题目:
给定两个字符串 s 和 t,判断它们是否是同构的。
如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。
每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序(⭐️)。不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身。
可以假设 s 和 t 长度相同。
示例 1:
输入:s = "egg", t = "add"
输出:true
示例 2:
输入:s = "foo", t = "bar"
输出:false
分析:
方法一:index
两字符串中映射字母的index应该相同才能是同构字符串(每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序)。
方法二:哈希表
使用两个map 保存 s[i] 到 t[i] 和 t[i] 到 s[i] 的映射关系,如果发现对应不上,立刻返回 false
代码:
// 方法一 index
public boolean isIsomorphic(String s, String t) {
char[] sArr = s.toCharArray();
char[] tArr = t.toCharArray();
for(int i=0;i<s.length();i++){
if(s.indexOf(sArr[i])!=t.indexOf(tArr[i])){
return false;
}
}
return true;
}
// 方法二 哈希表
public boolean isIsomorphic(String s, String t) {
Map<Character, Character> map1 = new HashMap<>();
Map<Character, Character> map2 = new HashMap<>();
for (int i = 0; i < s.length(); i++) {
if (!map1.containsKey(s.charAt(i))) {
map1.put(s.charAt(i), t.charAt(i)); // map1保存 s[i] 到 t[i]的映射
}
if (!map2.containsKey(t.charAt(i))) {
map2.put(t.charAt(i), s.charAt(i)); // map2保存 t[i] 到 s[i]的映射
}
// 无法映射,返回 false
if (map1.get(s.charAt(i)) != t.charAt(i) || map2.get(t.charAt(i)) != s.charAt(i)) {
return false;
}
}
return true;
}
206 反转链表
- 简单
- 2021.12.21:😎
题目:
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
分析:
方法一:迭代
在遍历列表时,将当前节点的 next 指针改为指向前一个元素。由于节点没有引用其上一个节点,因此必须事先存储其前一个元素。在更改引用之前,还需要另一个指针来存储下一个节点。不要忘记在最后返回新的头引用。
方法二:递归
为什么反转单链表可以用递归实现:
- 大问题拆成两个子问题
- 子问题求解方式和大问题一致
- 存在最小子问题
递的过程:
归的过程:需要完成反转这个动作
代码:
// 方法一-迭代
public ListNode reverseList(ListNode head) {
ListNode pre = null; // 由于节点没有引用其上一个节点,因此必须事先存储其前一个元素
ListNode cur = head;
while(cur!=null){
ListNode temp = cur.next; // 在更改引用之前,还需要另一个指针来存储下一个节点
cur.next = pre;
pre = cur;
cur = temp;
}
return pre;
}
// 方法二-递归
public ListNode reverseList(ListNode head) {
// 递归终止条件
if (head == null || head.next == null) {
return head;
}
ListNode p = reverseList(head.next); // 递归的过程
// 归-反转
head.next.next = head;
head.next = null;
return p;
}
#208. 实现 Trie (前缀树)
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#215. 数组中的第K个最大元素
- easy
- 2019.08.28:😭
- 2021.03.06:😎
- 2021.03.07:😎 随机枢纽点
题目:
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
分析:
方法一:基于快速排序的选择方法
适用于确定数据量的情况
我们可以用快速排序来解决这个问题,先对原数组排序,再返回倒数第 k 个位置,这样平均时间复杂度是O(nlogn),但其实我们可以做的更快。

因此我们可以改进快速排序算法来解决这个问题:在分解的过程当中,我们会对子数组进行划分,如果划分得到的 q 正好就是我们需要的下标,就直接返回 a[q];否则,如果 q 比目标下标小,就递归右子区间,否则递归左子区间。这样就可以把原来递归两个区间变成只递归一个区间,提高了时间效率。这就是「快速选择」算法。
我们知道快速排序的性能和「划分」出的子数组的长度密切相关。直观地理解如果每次规模为 n 的问题我们都划分成 1 和 n - 1,每次递归的时候又向 n−1 的集合中递归,这种情况是最坏的,时间代价是 $O(n^2)$。我们可以引入随机化来加速这个过程,它的时间代价的期望是 O(n)。
- 时间复杂度:O(n)
- 空间复杂度:O(nlogn)
方法二:堆排序
代码:
// 方法一:快速选择
class Solution {
Random random = new Random();
public int findKthLargest(int[] nums, int k) {
// 要找到的元素所在索引: 前K大,即倒数索引第K个
int index = nums.length - k;
int right = nums.length - 1;
int left = 0;
return quickSelect(nums, left, right, index);
}
public int quickSelect(int[] nums, int left, int right, int index) {
// 随机生成轴值,得到分区值后的轴值索引
int q = randomPartition(nums, left, right);
// 递归的出口
if (q == index) {
// 如果刚好索引q就是想要的索引,则直接返回
return nums[q];
} else {
// 如果不是,比较q 与 index ,确定下次要检索的区间, 要么是[q+1, right], 要么就是[left, q-1]
return q < index ? quickSelect(nums, q + 1, right, index) : quickSelect(nums, left, q - 1, index);
}
}
// 随机选择轴值
public int randomPartition(int[] nums, int l, int r) {
// 1. 随机数范围: [0, r-l+1) 同时加l, 则是 [l, r+1).即在这个[l,r] 中随机选一个索引出来
int i = random.nextInt(r - l + 1) + l;
// 2. 交换nums[i], nums[r], 也就是将随机数先放在最右边nums[r]上
swap(nums, i, r);
return partition(nums, l, r);
}
// 该函数负责把比轴值大的元素放到右边,小的元素放到左边,最后返回新数组中轴值的下标
// 为了方便比较,把轴值反倒数组的最右边,并且初始化第一个比轴值小的位置(数组的最左边)
public int partition(int[] nums, int l, int r) {
// 3. 在调用当前方法的randomPartition方法中,已经确定了随机数是nums[r]
int x = nums[r];
int i = l - 1; // i+1 为当前大于轴值的元素下标
// 首先比较区间在[l, r)之间
// 这个for循环操作就是将小于 x 的数都往[i, j]的左边区间设置,从而实现存在[l, i]区间,使得对应数值都 小于 x
for (int j = l; j < r; j++) {
// 4. nums[j] 跟随机数 x 比较
if (nums[j] <= x) {
i++; // 有小于x的元素,这轴值坐标+1
swap(nums, i, j);
}
}
// 换回轴值
//5. 既然已经将<x的值都放在一边了,现在将x也就是nums[r] 跟nums[i+1]交换,从而分成两个区间[l.i+1]左, [i+2, r]右,左边区间的值都小于x
swap(nums, i + 1, r);
// 然后返回这个分区值(新的初始索引left)
return i + 1;
}
public void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
#225. 用队列实现栈
- 简单
- 2021.03.20:😎
题目:
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通队列的全部四种操作(push、top、pop 和 empty)。
分析:
方法一:
代码:
Queue<Integer> queue1;
Queue<Integer> queue2;
/** Initialize your data structure here. */
public MyStack() {
queue1 = new LinkedList<Integer>();
queue2 = new LinkedList<Integer>();
}
/** Push element x onto stack. */
public void push(int x) {
queue2.offer(x);
while (!queue1.isEmpty()) {
queue2.offer(queue1.poll());
}
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue1.poll();
}
/** Get the top element. */
public int top() {
return queue1.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue1.isEmpty();
}
#226. 翻转二叉树
- easy
- 2020.10.01:😎
- 2020.10.27:😎 前序遍历写成了后序,也可以实现
题目:
翻转一棵二叉树。
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9
输出:
4
/ \
7 2
/ \ / \
9 6 3 1
分析:
通过观察,我们发现只要把二叉树上的每一个节点的左右子节点进行交换,最后的结果就是完全翻转之后的二叉树。
代码:
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root==null) return null;
/**** 前序遍历位置 ****/
// root 节点需要交换它的左右子节点
TreeNode temp = root.left;
root.left=root.right;
root.right=temp;
// 让左右子节点继续翻转它们的子节点
invertTree(root.left);
invertTree(root.right);
return root;
}
}
#230. 二叉搜索树中第K小的元素
- Medium
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#235. 二叉搜索树的最近公共祖先
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#236. 二叉树的最近公共祖先
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
242. 有效的字母异位词
- 简单
- 2021.11.27:
题目:
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false
分析:
方法一:排序
方法二:哈希表
- 首先判断两个字符串长度是否相等,不相等则直接返回 false
- 若相等,则初始化 26 个字母哈希表,遍历字符串 s 和 t
- s 负责在对应位置增加,t 负责在对应位置减少
- 如果哈希表的值都为 0,则二者是字母异位词
代码:
// 方法一
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
char[] str1 = s.toCharArray();
char[] str2 = t.toCharArray();
Arrays.sort(str1);
Arrays.sort(str2);
return Arrays.equals(str1, str2);
}
// 方法二
public boolean isAnagram(String s, String t) {
if(s.length()!=t.length()) return false;
int[] table = new int[26];
for(int i=0;i<s.length();i++){
table[s.charAt(i)-'a']++;
table[t.charAt(i)-'a']--;
}
for(int i:table){
if(i!=0) return false;
}
return true;
}
#287. 寻找重复数
- 中等
- 2021.04.11:😎
题目:
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,找出 这个重复的数 。
分析:
方法一:
代码:
#300. 最长递增子序列
最长递减子序列 = 翻转数组后求最长递增子序列
- 中等
- 2020.12.02:😭
题目:
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
分析:
最长递增子序列(Longest Increasing Subsequence,简写 LIS)是比较经典的一个问题,比较容易想到的是动态规划解法,时间复杂度 O(N^2),我们借这个问题来由浅入深讲解如何写动态规划。
我们的定义是这样的:dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。
举个例子:
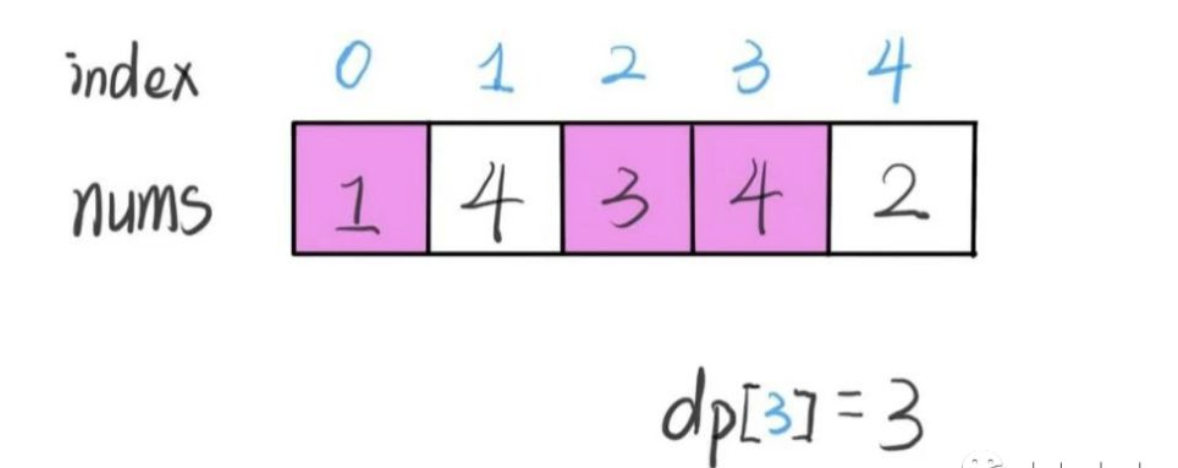
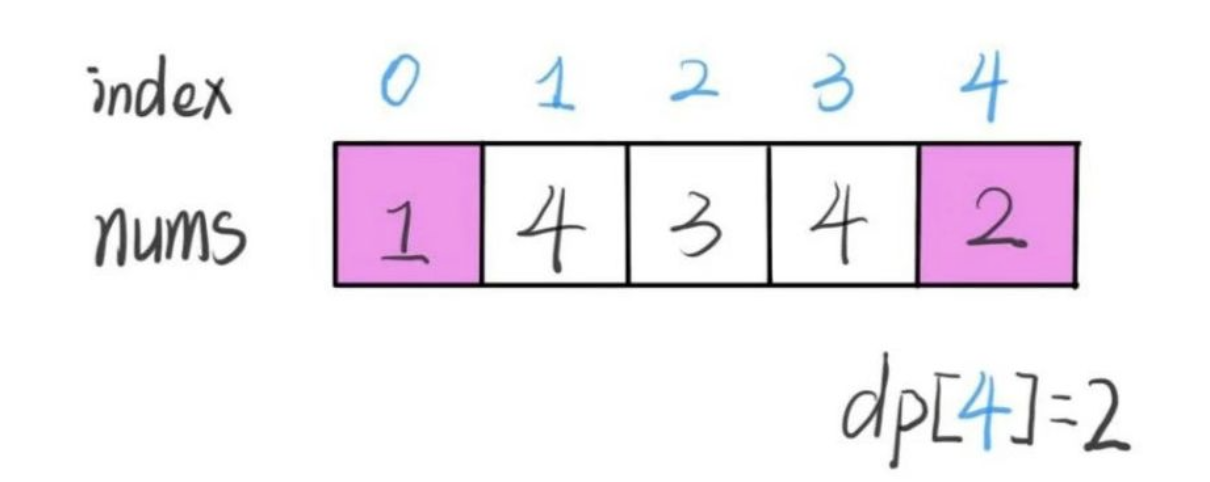
算法演进的过程是这样的:
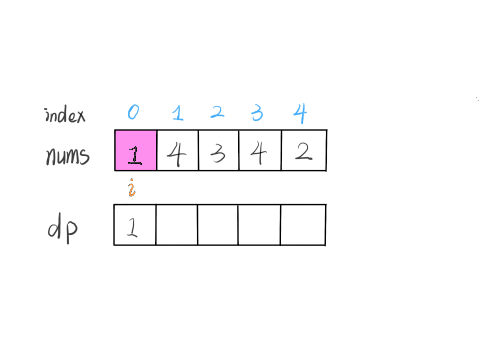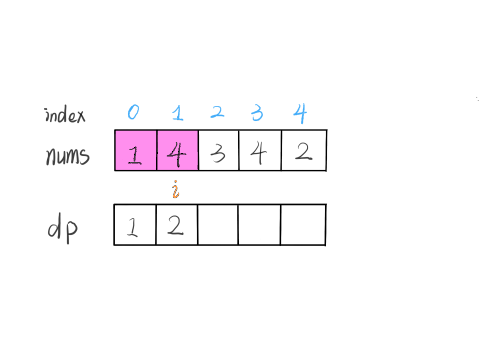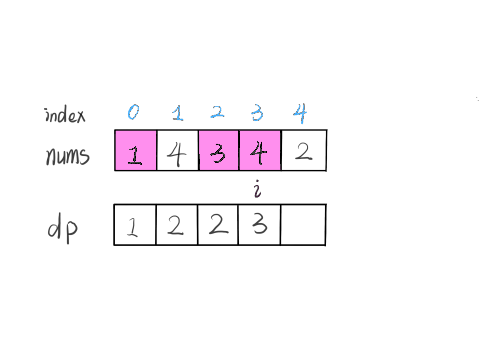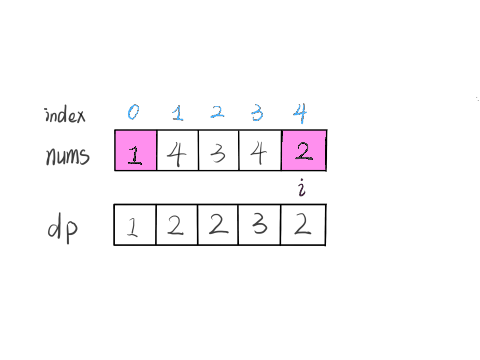
根据这个定义,我们的最终结果(子序列的最大长度)应该是 dp 数组中的最大值。
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
读者也许会问,刚才这个过程中每个 dp[i] 的结果是我们肉眼看出来的,我们应该怎么设计算法逻辑来正确计算每个 dp[i] 呢?
这就是动态规划的重头戏了,要思考如何进行状态转移,这里就可以使用数学归纳的思想:
我们已经知道了 dp[0...4] 的所有结果,我们如何通过这些已知结果推出 dp[5] 呢?
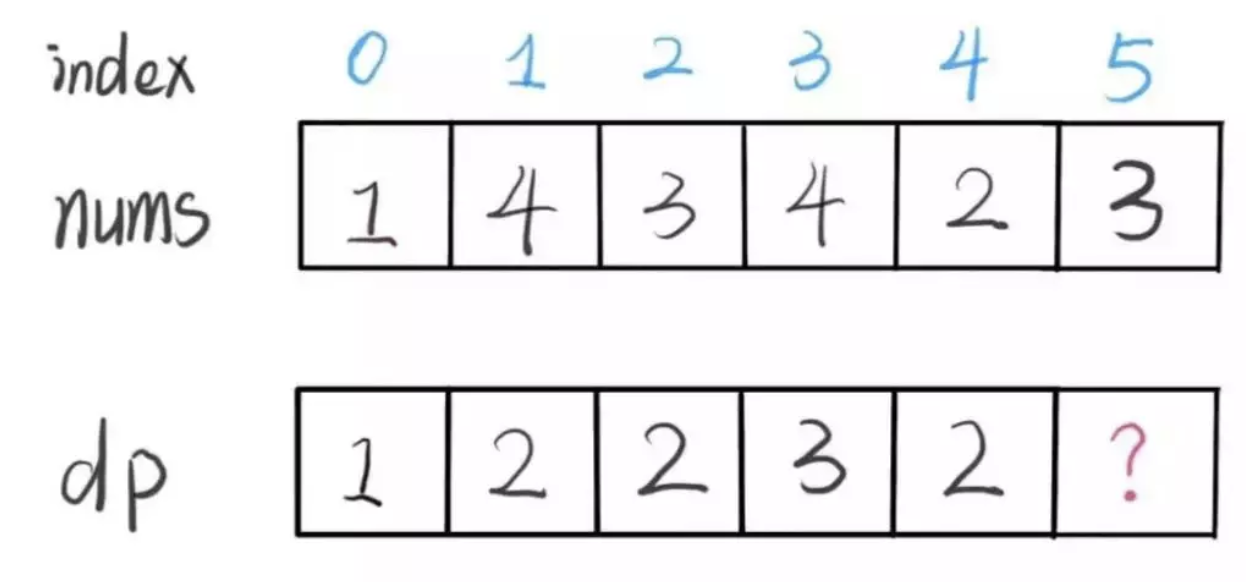
根据刚才我们对 dp 数组的定义,现在想求 dp[5] 的值,也就是想求以 nums[5] 为结尾的最长递增子序列。
nums[5] = 3,既然是递增子序列,我们只要找到前面那些结尾比 3 小的子序列,然后把 3 接到最后,就可以形成一个新的递增子序列,而且这个新的子序列长度加一。
当然,可能形成很多种新的子序列,但是我们只要最长的,把最长子序列的长度作为 dp[5] 的值即可。
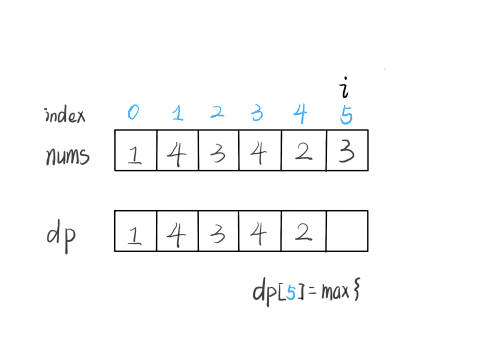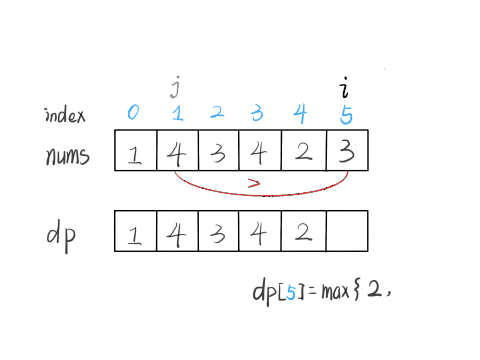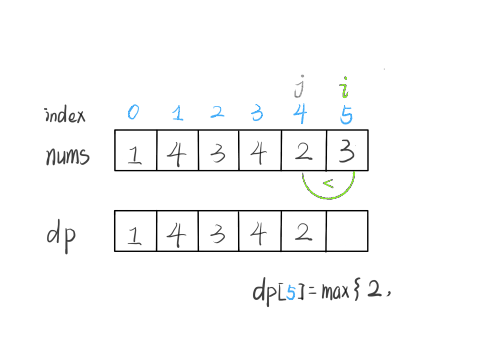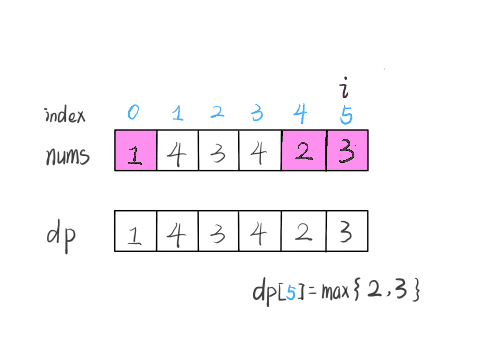

这段代码的逻辑就可以算出 dp[5]。到这里,这道算法题我们就基本做完了。读者也许会问,我们刚才只是算了 dp[5] 呀,dp[4], dp[3] 这些怎么算呢?
类似数学归纳法,你已经可以通过 dp[0…4] 算出 dp[5] 了,那么任意 dp[i] 你肯定都可以算出来:

还有一个细节问题,就是 base case ;dp 数组应该全部初始化为 1,因为子序列最少也要包含自己,所以长度最小为 1。下面我们看一下完整代码:
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp, 1); // base case ;dp 数组应该全部初始化为 1,因为子序列最少也要包含自己,所以长度最小为 1
for (int i = 0; i < nums.length; i++) { // 根据当前位置i的前几项推出dp[i]的值
for (int j = 0; j < i; j++) {
if (nums[j]<nums[i]) {
dp[i]=Math.max(dp[i],dp[j]+1);
}
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res,dp[i]);
}
return res;
}
}
至此,这道题就解决了,时间复杂度 O(N^2)。总结一下动态规划的设计流程:
首先明确 dp 数组所存数据的含义。这步很重要,如果不得当或者不够清晰,会阻碍之后的步骤。
然后根据 dp 数组的定义,运用数学归纳法的思想,假设 dp[0…i−1] 都已知,想办法求出 dp[i],一旦这一步完成,整个题目基本就解决了。
但如果无法完成这一步,很可能就是 dp 数组的定义不够恰当,需要重新定义 dp 数组的含义;或者可能是 dp 数组存储的信息还不够,不足以推出下一步的答案,需要把 dp 数组扩大成二维数组甚至三维数组。
动态规划+二分查找
很具小巧思。新建数组 track,用于保存最长上升子序列。
对原序列进行遍历,将每位元素二分插入 track 中。
如果 track 中元素都比它小,将它插到最后。否则,用它覆盖掉track数组中大于等于该元素中最小的那个元素。
总之,思想就是让 track 中存储比较小的元素。这样,track 未必是真实的最长上升子序列,但长度是对的。(总是致力于构造最小上升队列,让后面新的数更有可能累加上)
public int lengthOfLIS(int[] nums) {
int[] track = new int[nums.length];
int res = 0; // 当前track数组的长度
for(int num : nums) {
int l = -1, r = res;
while(l+1 != r) {
int m = (l + r) / 2;
if(track[m] < num) l = m;
else r = m;
}
track[r] = num;
if(r==res) res++; // 如果r=res表示没找到第一个大于num的数,将num插到最后。长度+1
}
return res;
}
#322. 零钱兑换
- 中等
- 2020.11.16:😭
- 2020.11.17:😭 忘记考虑了子问题无解!
题目:
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
分析:
方法一:暴力递归
首先,这个问题是动态规划问题,因为它具有「最优子结构」的。要符合「最优子结构」,子问题间必须互相独立。
凑零钱问题,为什么说它符合最优子结构呢?比如你想求 amount = 11 时的最少硬币数(原问题),如果你知道凑出 amount = 10 的最少硬币数(子问题),你只需要把子问题的答案加一(再选一枚面值为 1 的硬币)就是原问题的答案。因为硬币的数量是没有限制的,所以子问题之间没有相互制,是互相独立的。
那么,既然知道了这是个动态规划问题,就要思考如何列出正确的状态转移方程?
1、确定 base case,这个很简单,显然目标金额 amount 为 0 时算法返回 0,因为不需要任何硬币就已经凑出目标金额了。
2、确定「状态」,也就是原问题和子问题中会变化的变量。由于硬币数量无限,硬币的面额也是题目给定的,只有目标金额会不断地向 base case 靠近,所以唯一的「状态」就是目标金额 amount。
3、确定「选择」,也就是导致「状态」产生变化的行为。目标金额为什么变化呢,因为你在选择硬币,你每选择一枚硬币,就相当于减少了目标金额。所以说所有硬币的面值,就是你的「选择」。
4、明确 dp 函数/数组的定义。我们这里讲的是自顶向下的解法,所以会有一个递归的 dp 函数,一般来说函数的参数就是状态转移中会变化的量,也就是上面说到的「状态」;函数的返回值就是题目要求我们计算的量。就本题来说,状态只有一个,即「目标金额」,题目要求我们计算凑出目标金额所需的最少硬币数量。所以我们可以这样定义 dp 函数:
dp(n) 的定义:输入一个目标金额 n,返回凑出目标金额 n 的最少硬币数量。
搞清楚上面这几个关键点,解法的伪码就可以写出来了:
class Solution {
// 伪代码框架
public int coinChange(int[] coins, int amount) {
return dp(coins,amount);
}
// 定义:要凑出金额n,至少需要dp(n)个硬币
public int dp(int[] coins,int amount){
int res = Integer.MAX_VALUE;
// 做选择,选择需要硬币最少的那个结果
for (int coin : coins) {
res=Math.min(res,1+dp(coins,amount-coin));
}
return res;
}
}
根据伪码,我们加上 base case 即可得到最终的答案。显然目标金额为 0 时,所需硬币数量为 0;当目标金额小于 0 时,无解,返回 -1:
class Solution {
// 伪代码框架
public int coinChange(int[] coins, int amount) {
return dp(coins,amount);
}
// 定义:要凑出金额n,至少需要dp(n)个硬币
public int dp(int[] coins,int amount){
// base case
if (amount==0) return 0;
if (amount<0) return -1;
// 求最小值,使用初始化为Integer的最大值
int res = Integer.MAX_VALUE;
for (int coin : coins) {
int subProblem = dp(coins,amount-coin);
// 子问题无解 跳过
if (subProblem==-1) continue;
res=Math.min(res,1+subProblem);
}
return res!=Integer.MAX_VALUE?res:-1;
}
}
至此,状态转移方程其实已经完成了,以上算法已经是暴力解法了,以上代码的数学形式就是状态转移方程:
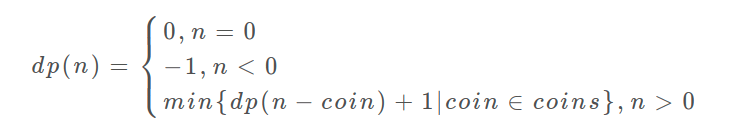
至此,这个问题其实就解决了,只不过需要消除一下重叠子问题,比如 amount = 11, coins = {1,2,5} 时画出递归树看看:
递归算法的时间复杂度分析:子问题总数 x 每个子问题的时间。
子问题总数为递归树节点个数,这个比较难看出来,是 O(n^k),总之是指数级别的。每个子问题中含有一个 for 循环,复杂度为 O(k)。所以总时间复杂度为 O(k * n^k),指数级别。
方法二:带备忘录的递归
类似之前斐波那契数列的例子,只需要稍加修改,就可以通过备忘录消除子问题.
很显然「备忘录」大大减小了子问题数目,完全消除了子问题的冗余,所以子问题总数不会超过金额数 n,即子问题数目为 O(n)。处理一个子问题的时间不变,仍是 O(k),所以总的时间复杂度是 O(kn)。
class Solution {
// 伪代码框架
public int coinChange(int[] coins, int amount) {
// 初始化备忘录
HashMap<Integer, Integer> memo = new HashMap<>();
return dp(memo,coins,amount);
}
// 定义:要凑出金额n,至少需要dp(n)个硬币
public int dp(HashMap<Integer, Integer> memo,int[] coins,int amount){
// 查备忘录,避免重复计算
Integer integer = memo.get(amount);
if (integer !=null) return integer;
// base case
if (amount==0) return 0;
if (amount<0) return -1;
// 求最小值,使用初始化为Integer的最大值
int res = Integer.MAX_VALUE;
for (int coin : coins) {
int subProblem = dp(memo,coins,amount-coin);
// 子问题无解 跳过
if (subProblem==-1) continue;
res=Math.min(res,1+subProblem);
}
// 记录备忘录
memo.put(amount,res!=Integer.MAX_VALUE?res:-1);
return memo.get(amount);
}
}
方法三:
weight数组在本题中就是硬币的面额coins;value数组则都是1;求value的最小值
完全背包最值问题:外循环物品coins,内循环背包容量amount正序且背包容量target >= coins[i]。
class Solution {
public int coinChange(int[] coins, int amount) {
// dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
int[] dp = new int[amount + 1];
// 考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
for (int j = 0; j <= amount; j++) {
dp[j] = Integer.MAX_VALUE;
}
// base case:首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0
dp[0] = 0;
// 确定遍历顺序:完全背包最值问题-外循环物品coins,内循环背包容量amount正序
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++) {
if (dp[j - coins[i]] != Integer.MAX_VALUE) { //只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount] == Integer.MAX_VALUE?-1:dp[amount];
}
}
#337. 打家劫舍 III
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#345. 反转字符串中的元音字符
- Easy
- 2019.09.11:😎
- 2019.09.12:😭 temp变量没定义,判断写成了
chars.indexOf(s[i]!=-1); - 2021.03.05:😎
题目:
编写一个函数,以字符串作为输入,反转该字符串中的元音字母。
示例 1:
输入:"hello"
输出:"holle"
分析:
双指针法交换前后元音元素
转换成数组后,分别定义前后两个索引指针用 while 依次遍历数组,同时遇到元音则交换。
最后扫描完数组后,一定要在返回的时候再转成字符串 String 输出
代码:
class Solution {
public String reverseVowels(String s) {
String targetStr = "aeuioAEUIO";
char[] strArr = s.toCharArray();
int low = 0;int high = strArr.length-1;
while(low<high){
// 左指针找到第一个元音字母 注意一定要保持low<high
while(targetStr.indexOf(strArr[low])==-1 && low<high){
low++;
}
// 右指针找到第一个元音字母
while(targetStr.indexOf(strArr[high])==-1&&low<high){
high--;
}
// 如果在low<high的情况下找到了两个元音字母便交换
if(low<high){
char temp = strArr[low];
strArr[low]=strArr[high];
strArr[high]=temp;
low++;
high--;
}
}
return new String(strArr);
}
}
#347. 前 K 个高频元素
- medium
- 2019.09.23:😭
题目:
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示:
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
你可以按任意顺序返回答案。
分析:
方法一:粗暴排序法 使用排序算法对元素按照频率由高到低进行排序,然后再取前 k 个元素。使用常规的诸如 冒泡、选择、甚至快速排序都是不满足题目要求,它们的时间复杂度都是大于或者等于 O(nlogn),而题目要求算法的时间复杂度必须优于 O(nlogn)。
方法二:最小堆 题目最终需要返回的是前 k 个频率最大的元素,可以想到借助堆这种数据结构,对于 k 频率之后的元素不用再去处理,进一步优化时间复杂度。
 具体操作为:
具体操作为:
- 借助 哈希表 来建立数字和其出现次数的映射,遍历一遍数组统计元素的频率
- 维护一个元素数目为 k 的最小堆
- 每次都将新的元素与堆顶元素(堆中频率最小的元素)进行比较
- 如果新的元素的频率比堆顶端的元素大,则弹出堆顶端的元素,将新的元素添加进堆中
- 最终,堆中的 k 个元素即为前 k 个高频元素
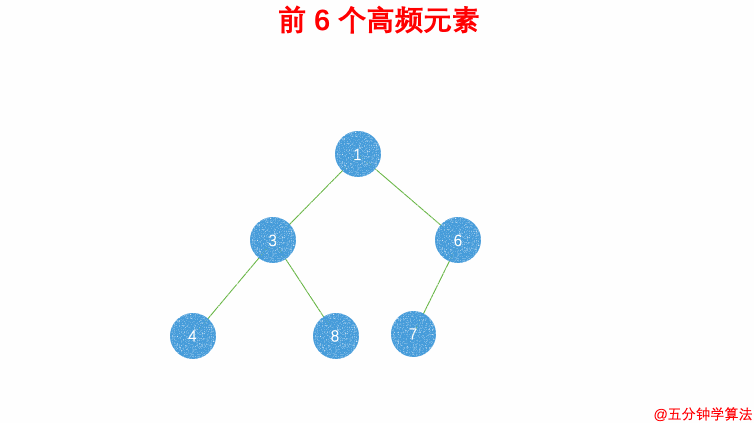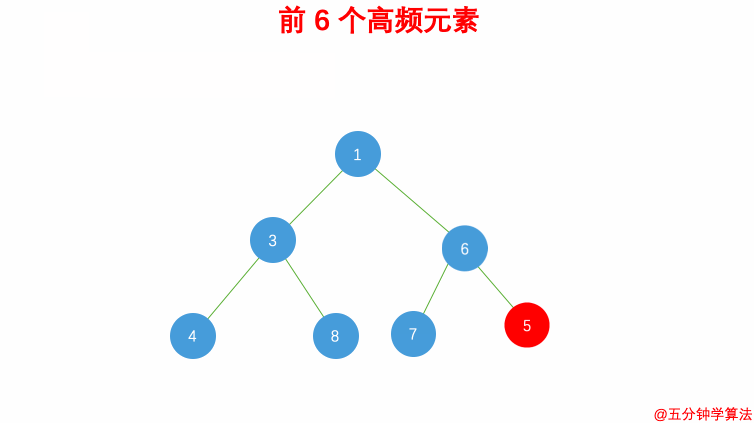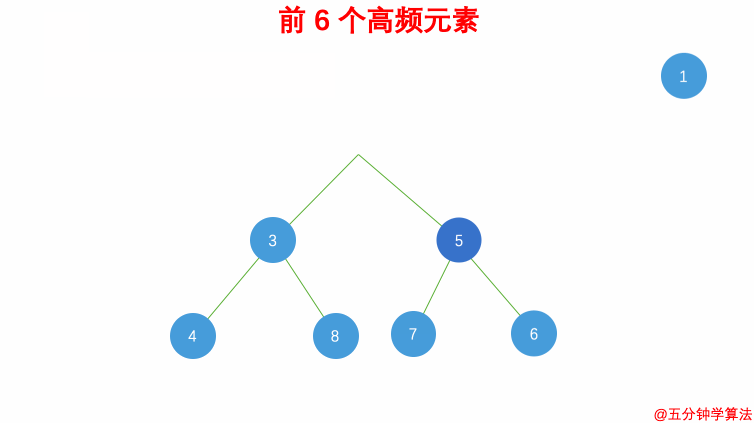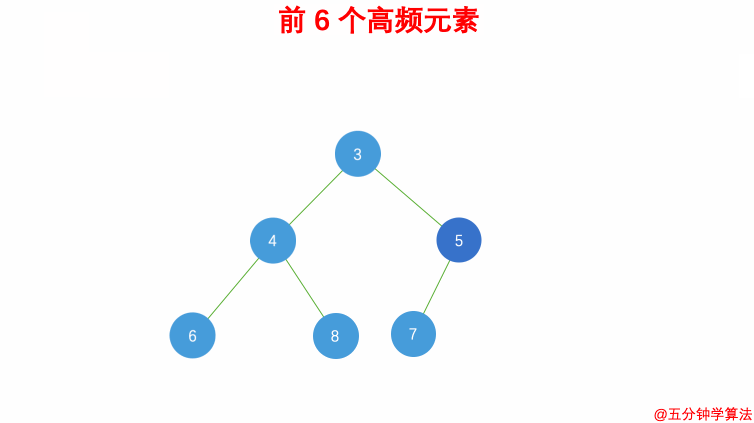
方法三:桶排序法 首先依旧使用哈希表统计频率,统计完成后,创建一个数组,将频率作为数组下标,对于出现频率不同的数字集合,存入对应的数组下标即可。
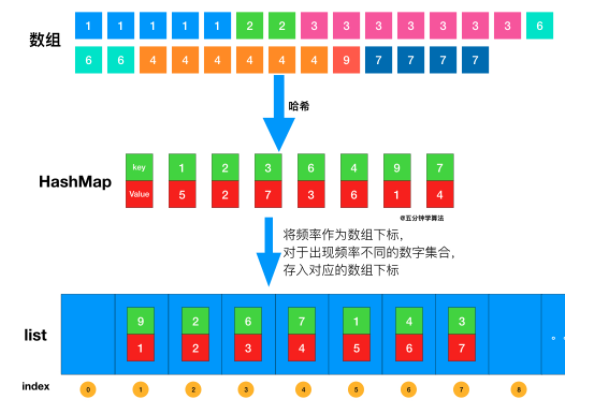
代码:
// 方法二
class Solution {
public List<Integer> topKFrequent(int[] nums, int k) {
// 使用字典,统计每个元素出现的次数,元素为键,元素出现的次数为值
HashMap<Integer,Integer> map = new HashMap();
for(int num : nums){
if (map.containsKey(num)) {
map.put(num, map.get(num) + 1);
} else {
map.put(num, 1);
}
}
// 遍历map,用最小堆保存频率最大的k个元素
PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> map.get(a) - map.get(b));
for (Integer key : map.keySet()) {
if (pq.size() < k) {
pq.add(key);
} else if (map.get(key) > map.get(pq.peek())) {
pq.remove();
pq.add(key);
}
}
// 取出最小堆中的元素
List<Integer> res = new ArrayList<>();
while (!pq.isEmpty()) {
res.add(pq.remove());
}
return res;
}
}
// 方法三
class Solution {
public int[] topKFrequent(int[] nums, int k) {
List<Integer> res = new ArrayList();
// 使用字典,统计每个元素出现的次数,元素为键,元素出现的次数为值
HashMap<Integer, Integer> map = new HashMap<>();
for(int key:nums){
map.put(key,map.getOrDefault(key,0)+1);
}
// 桶排序 将频率作为数组下标,对于出现频率不同的数字集合,存入对应的数组下标
// 把频率作为桶/数组下标,再存入对应的数
List<Integer>[] list = new List[nums.length+1]; // 最大频率为nums.length
for (Integer key : map.keySet()) {
// 获取出现的次数作为下标
int i = map.get(key);
if (list[i]==null){
list[i]=new ArrayList<>();
}
list[i].add(key);
}
// 倒序遍历数组获取出现顺序从大到小的排列
for(int i = list.length - 1;i >= 0 && res.size() < k;i--){
if(list[i] == null) continue;
res.addAll(list[i]);
}
// list转数组
int[] arr = new int[k];
for (int i = 0; i < k); i++) {
arr[i]=res.get(i);
}
return arr;
}
}
#349. 两个数组的交集
- 简单
- 2021.04.11:😭
题目:
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
分析:
方法一:哈希表
方法二:排序 +双指针
如果两个数组是有序的,则可以使用双指针的方法得到两个数组的交集。
首先对两个数组进行排序,然后使用两个指针遍历两个数组。可以预见的是加入答案的数组的元素一定是递增的,为了保证加入元素的唯一性,我们需要额外记录变量 pre 表示上一次加入答案数组的元素。
初始时,两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字,如果两个数字不相等,则将指向较小数字的指针右移一位,如果两个数字相等,且该数字不等于 pre ,将该数字添加到答案并更新 pre 变量,同时将两个指针都右移一位。当至少有一个指针超出数组范围时,遍历结束。
代码:
// 空间换时间
public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> set = new HashSet<>();
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : nums1) {
map.put(num,map.getOrDefault(num,0)+1);
}
for (int num : nums2) {
if (map.get(num)!=null){
set.add(num);
}
}
int index = 0;
int[] res = new int[set.size()];
for (Integer integer : set) {
res[index++] = integer;
}
return res;
}
// 排序 + 双指针
public int[] intersection(int[] nums1, int[] nums2) {
Arrays.sort(nums1);
Arrays.sort(nums2);
int index=0,index1 = 0,index2=0;
int len1 = nums1.length,len2 = nums2.length;
int[] res = new int[len1+len2];
while (index1<len1&&index2<len2){
if (nums1[index1]==nums2[index2]){
if (index==0||nums1[index1]!=res[index-1]){
res[index]=nums1[index1];
index++;
}
index1++;
index2++;
}else if (nums1[index1]<nums2[index2]){
index1++;
}else {
index2++;
}
}
return Arrays.copyOf(res,index);
}
#354. 俄罗斯套娃信封问题
- 中等
- 2020.12.02:😭
题目:
给定一些标记了宽度和高度的信封,宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
说明:
不允许旋转信封。
示例:
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出: 3
解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
分析:
这道题目其实是最长递增子序列(Longes Increasing Subsequence,简写为 LIS)的一个变种,因为很显然,每次合法的嵌套是大的套小的,相当于找一个最长递增的子序列,其长度就是最多能嵌套的信封个数。
但是难点在于,标准的 LIS 算法只能在数组中寻找最长子序列,而我们的信封是由 (w, h) 这样的二维数对形式表示的,如何把 LIS 算法运用过来呢?

读者也许会想,通过 w × h 计算面积,然后对面积进行标准的 LIS 算法。但是稍加思考就会发现这样不行,比如 1 × 10 大于 3 × 3,但是显然这样的两个信封是无法互相嵌套的。
这道题的解法是比较巧妙的:
先对宽度 w 进行升序排序,如果遇到 w 相同的情况,则按照高度 h 降序排序。之后把所有的 h 作为一个数组,在这个数组上计算 LIS 的长度就是答案。
画个图理解一下,先对这些数对进行排序:

然后在 h 上寻找最长递增子序列:

这个子序列就是最优的嵌套方案。
这个解法的关键在于,对于宽度 w 相同的数对,要对其高度 h 进行降序排序。因为两个宽度相同的信封不能相互包含的,逆序排序保证在 w 相同的数对中最多只选取一个。
下面看代码:
// envelopes = [[w, h], [w, h]...]
public int maxEnvelopes(int[][] envelopes) {
int n = envelopes.length;
// 按宽度升序排列,如果宽度一样,则按高度降序排列
// [5,4],[6,4],[6,7],[2,3] --> [2,3],[5,4],[6,4],[6,7]
// w相等则比较h(h小在后),不想等直接比较w(w小在前)
Arrays.sort(envelopes, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);
// 对高度数组寻找 LIS
int[] height = new int[n];
for (int i = 0; i < n; i++)
height[i] = envelopes[i][1];
return lengthOfLIS(height);
关于最长递增子序列的寻找方法,在前文中详细介绍了动态规划解法,直接套用算法模板:
/* 返回 nums 中 LIS 的长度 */
public int lengthOfLIS(int[] height) {
int[] dp = new int[height.length];
Arrays.fill(dp, 1); // base case ;dp 数组应该全部初始化为 1,因为子序列最少也要包含自己,所以长度最小为 1
for (int i = 0; i < nums.length; i++) { // 根据当前位置i的前几项推出dp[i]的值
for (int j = 0; j < i; j++) {
if (height[j]<height[i]) {
dp[i]=Math.max(dp[i],dp[j]+1);
}
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res,dp[i]);
}
return res;
}
为了清晰,我将代码分为了两个函数, 你也可以合并,这样可以节省下 height 数组的空间。
#404. 左叶子之和
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
409. 最长回文串
- 简单
- 2021.11.27:
题目:
给定一个包含大写字母和小写字母的字符串,找到通过这些字母构造成的最长的回文串。
在构造过程中,请注意区分大小写。比如 "Aa" 不能当做一个回文字符串。
示例 1:
输入:
"abccccdd"
输出:
7
解释:
我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。
分析:
方法一:
遍历字符串, 只能出现一个次数为奇数的字符,所以我们直接记录有多少个字符出现次数为奇数就可以了。
代码:
// ASCLL码,十进制的话,共128个
public int longestPalindrome(String s) {
int[] arr = new int[128];
int len = s.length();
for(char c : s.toCharArray()) {
arr[c]++;
}
int count = 0;
for (int i : arr) {
if(i%2==1){
count++;
}
}
return count == 0 ? len : (len - count + 1);
}
#416. 分割等和子集
- 中等
题目:
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
分析:
0-1背包存在性问题:是否存在一个子集,其和为target=sum/2,外循环nums,内循环target倒序
具体实现参考 #494-目标和
代码:
// 方法一:类似于目标和,看作是组合问题。>0则是存在
public boolean canPartition(int[] nums) {
int sum = Arrays.stream(nums).sum();
if(sum%2==1) {
return false;
}
return dp(nums,sum/2);
}
// weight:nums bagWeight:target
boolean dp(int[] nums,int target){
// 初始化
int n = nums.length;
int[] dp = new int[target+1];
// 因为背包没有空间的时候,就相当于装满了,也是一种装法
dp[0]=1;
// dp公式 dp[j] = dp[j] + dp[j-nums[i]];
// 0-1问题,先遍历物品再遍历背包,倒序且>nums[i]
for(int i=0;i<nums.length;i++){
for(int j=target;j>=nums[i];j--){
dp[j] += dp[j-nums[i]];
}
}
return dp[target] != 0;
}
// 方法二:看作是0-1背包存在性问题-是否存在一个子集,其和为target=sum/2,外循环nums,内循环target倒序
public boolean canPartition(int[] nums) {
int sum = Arrays.stream(nums).sum();
if(sum%2==1) {
return false;
}
return dp(nums,sum/2);
}
// weight:nums bagWeight:target
boolean dp(int[] nums,int target){
// 初始化
int n = nums.length;
boolean[] dp = new boolean[target+1];
dp[0]=true;
// dp公式 dp[j] = dp[j] + dp[j-nums[i]];
// 0-1问题,先遍历物品再遍历背包,倒序且>nums[i]
for(int i=0;i<nums.length;i++){
for(int j=target;j>=nums[i];j--){
dp[j] = dp[j] || dp[j - nums[i]];
}
}
return dp[target];
}
#435. 无重叠区间
- 中等
- 2021.04.08:😎
题目:
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
分析:
方法一:贪心思想
我们已经会求最多有几个区间不会重叠了,那么剩下的不就是至少需要去除的区间吗
代码:
public int eraseOverlapIntervals(int[][] intervals) {
int len = intervals.length;
if(len==0) return 0;
Arrays.sort(intervals,(a,b)->a[1]-b[1]);
int count = 1;
int xEnd = intervals[0][1];
for (int[] intv : intervals) {
int start = intv[0];
if (start>=xEnd){
count++;
xEnd = intv[1];
}
}
return len-count;
}
#437. 路径总和 III
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#438. 找到字符串中所有字母异位词
- 中等
- 2020.12.02:😭
- 2021.03.06:😭 收缩判断条件错误,window更新值要在valid验证之后。
题目:
给定一个字符串 s 和一个非空字符串 p,找到 s 中所有是 p 的字母异位词的子串,返回这些子串的起始索引。
字符串只包含小写英文字母,并且字符串 s 和 p 的长度都不超过 20100。
说明:
字母异位词指字母相同,但排列不同的字符串。
不考虑答案输出的顺序。
示例 1:
输入:
s: "cbaebabacd" p: "abc"
输出:
[0, 6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。
分析:
这个所谓的字母异位词,不就是排列吗,搞个高端的说法就能糊弄人了吗?相当于,输入一个串 S,一个串T,找到 S 中所有 T 的排列,返回它们的起始索引。
直接默写一下框架,明确刚才讲的 4 个问题,即可秒杀这道题:
跟寻找字符串的排列一样,只是找到一个合法异位词(排列)之后将起始索引加入 res 即可。
代码:
public List<Integer> findAnagrams(String s, String p) {
// 结果列表
ArrayList<Integer> result = new ArrayList<>();
// need window hashMap
// 初始化need
HashMap<Character, Integer> need = new HashMap<>();
HashMap<Character, Integer> window = new HashMap<>();
for (char key : p.toCharArray()) {
need.put(key, need.getOrDefault(key, 0) + 1);
}
// 窗口指针 统计参数valid
int left = 0;
int right = 0;
int valid = 0;
// 开始滑动
char[] sArray = s.toCharArray();
while (right < s.length()) {
// right 增加
Character c = sArray[right];
right++;
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c))) {
valid++;
}
}
// left++ 收缩条件?窗口大小>=p.length()
while ((right - left) >= p.length()) {
// 处理逻辑
if (valid == need.size()) {
result.add(left);
}
// 更新参数
Character d = sArray[left];
left++;
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.get(d) - 1);
}
}
}
return result;
}
#451. 根据字符出现频率排序
- easy
- 2019.08.28:😭
题目:
给定一个字符串,请将字符串里的字符按照出现的频率降序排列。
示例 1:
输入:
"tree"
输出:
"eert"
解释:
'e'出现两次,'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外,"eetr"也是一个有效的答案。
分析:
桶排序
代码:
class Solution {
public String frequencySort(String s) {
if (s.isEmpty() || s.length() == 1) {
return s;
}
// 桶排序
// 散列表统计各个字符的频率
HashMap<Character,Integer> map = new HashMap<>();
for(char ch: s.toCharArray()){
map.put(ch,map.getOrDefault(ch,0)+1);
}
// 根据频率放入对应的桶 最大频率为s.length()
List<Character>[] bucket = new ArrayList[s.length()+1]; // 0号桶不用
for(char key:map.keySet()){
int value = map.get(key);
if(bucket[value]==null) bucket[value] = new ArrayList<Character>();
bucket[map.get(key)].add(key);
}
// 从后往前取出
StringBuilder res = new StringBuilder();
for(int i=s.length();i>0;i--){
if(bucket[i]!=null){
for(char ch:bucket[i]){
for (int k = i; k > 0; k--) {
// 字符出现了几次就向 res 中添加几次该字符
res.append(ch);
}
}
}
}
return res.toString();
}
}
#452. 用最少数量的箭引爆气球
- 中等
- 2021.04.08:
题目:
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]]
输出:4
分析:贪心思想
其实稍微思考一下,这个问题和区间调度算法一模一样!如果最多有 n 个不重叠的区间,那么就至少需要 n 个箭头穿透所有区间:
只是有一点不一样,在 intervalSchedule 算法中,如果两个区间的边界触碰,不算重叠;而按照这道题目的描述,箭头如果碰到气球的边界气球也会爆炸,所以说相当于区间的边界触碰也算重叠:
代码:
public int findMinArrowShots(int[][] points) {
if(points.length == 0) return 0;
Arrays.sort(points, (p1, p2) -> p1[1] < p2[1] ? -1 : 1); // 不要用 a[1] - b[1] 会溢出
int res = 1;
int pre = points[0][1];
for (int i = 1; i < points.length; i++) {
if (points[i][0] > pre) {
res++;
pre = points[i][1];
}
}
return res;
}
#460.LFU 缓存
- 困难
- 2021.03.13:😭
题目:
请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。
实现 LFUCache 类:
- LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
- int get(int key) - 如果键存在于缓存中,则获取键的值,否则返回 -1。
- void put(int key, int value) - 如果键已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量时,则应该在插入新项之前,使最不经常使用的项无效。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 最久未使用 的键。
注意「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。使用次数会在对应项被移除后置为 0 。
为了确定最不常使用的键,可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。
当一个键首次插入到缓存中时,它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作,使用计数器的值将会递增。
示例:
输入:
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出:
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]
解释:
// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序(最左边的元素是最近的)
LFUCache lFUCache = new LFUCache(2);
lFUCache.put(1, 1); // cache=[1,_], cnt(1)=1
lFUCache.put(2, 2); // cache=[2,1], cnt(2)=1, cnt(1)=1
lFUCache.get(1); // 返回 1
// cache=[1,2], cnt(2)=1, cnt(1)=2
lFUCache.put(3, 3); // 去除键 2 ,因为 cnt(2)=1 ,使用计数最小
// cache=[3,1], cnt(3)=1, cnt(1)=2
lFUCache.get(2); // 返回 -1(未找到)
lFUCache.get(3); // 返回 3
// cache=[3,1], cnt(3)=2, cnt(1)=2
lFUCache.put(4, 4); // 去除键 1 ,1 和 3 的 cnt 相同,但 1 最久未使用
// cache=[4,3], cnt(4)=1, cnt(3)=2
lFUCache.get(1); // 返回 -1(未找到)
lFUCache.get(3); // 返回 3
// cache=[3,4], cnt(4)=1, cnt(3)=3
lFUCache.get(4); // 返回 4
// cache=[3,4], cnt(4)=2, cnt(3)=3
分析:
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#494. 目标和
- 中等
- 2020.12.09:😭
题目:
给定一个非负整数数组,a1, a2, ..., an, 和一个目标数S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 - 中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例:
输入:nums: [1, 1, 1, 1, 1], S: 3
输出:5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
提示:
数组非空,且长度不会超过 20 。
初始的数组的和不会超过 1000 。
保证返回的最终结果能被 32 位整数存下。
分析:
方法一:回溯算法
任何算法的核心都是穷举,回溯算法就是一个暴力穷举算法,前文 回溯算法解题框架 就写了回溯算法框架:
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
关键就是搞清楚什么是「选择」,而对于这道题,「选择」不是明摆着的吗?对于每个数字 nums[i],我们可以选择给一个正号 + 或者一个负号 -,然后利用回溯模板穷举出来所有可能的结果,数一数到底有几种组合能够凑出 target 不就行了嘛?
如果看过我们之前的几篇回溯算法文章,这个代码可以说是比较简单的了:
int result = 0;
/* 主函数 */
int findTargetSumWays(int[] nums, int target) {
if (nums.length == 0) return 0;
backtrack(nums, 0, target);
return result;
}
/* 回溯算法模板 */
// i-nums[i]-记录当前路径到哪了 rest-目标值
void backtrack(int[] nums, int i, int rest) {
// base case
if (i == nums.length) {
if (rest == 0) {
// 说明恰好凑出 target
result++;
}
return;
}
// 给 nums[i] 选择 - 号
rest += nums[i];
// 穷举 nums[i + 1]
backtrack(nums, i + 1, rest);
// 撤销选择
rest -= nums[i];
// 给 nums[i] 选择 + 号
rest -= nums[i];
// 穷举 nums[i + 1]
backtrack(nums, i + 1, rest);
// 撤销选择
rest += nums[i];
}
有的读者可能问,选择 - 的时候,为什么是 rest += nums[i],选择 + 的时候,为什么是 rest -= nums[i] 呢,是不是写反了?
不是的,「如何凑出 target」和「如何把 target 减到 0」其实是一样的。我们这里选择后者,因为前者必须给 backtrack 函数多加一个参数sum,我觉得不美观:
void backtrack(int[] nums, int i, int sum, int target) {
// base case
if (i == nums.length) {
if (sum == target) {
result++;
}
return;
}
// ...
}
因此,如果我们给 nums[i] 选择 + 号,就要让 rest - nums[i],反之亦然。
以上回溯算法可以解决这个问题,时间复杂度为 O(2^N),N 为 nums 的大小,这个回溯算法就是个二叉树的遍历问题:
public int result = 0; // 方法数
public int findTargetSumWays(int[] nums, int S) {
backtrack(nums, 0, S);
return result;
}
// i-nums[i]-记录当前路径到哪了 rest-目标值
public void backtrack(int[] nums, int i, int rest) {
if (i == nums.length) {
if (rest == 0) {
// 说明恰好凑出 target
result++;
}
return;
}
backtrack(nums,i+1,rest-nums[i]);
backtrack(nums,i+1,rest+nums[i]);
}
树的高度就是 nums 的长度嘛,所以说时间复杂度就是这棵二叉树的节点数,为 O(2^N),其实是非常低效的。
那么,这个问题如何用动态规划思想进行优化呢?
方式二:动态规划
其实,这个问题可以转化为一个子集划分问题,而子集划分问题又是一个典型的背包问题。动态规划总是这么玄学,让人摸不着头脑……
首先,如果我们把 nums 划分成两个子集 A 和 B,分别代表分配 + 的数和分配 - 的数,那么他们和 target 存在如下关系:
sum(A) - sum(B) = target // 1
sum(A) = target + sum(B) // 2
sum(A) + sum(A) = target + sum(B) + sum(A) // 2式两边都加上Sum(A)
2 * sum(A) = target + sum(nums)
综上,可以推出 sum(A) = (target + sum(nums)) / 2,也就是把原问题转化成:nums 中存在几个子集 A,使得 A 中元素的和为 (target + sum(nums)) / 2?
类似的子集划分问题,实现这么一个函数:
/* 计算 nums 中有几个子集的和为 sum */
int subsets(int[] nums, int sum) {}
然后,可以这样调用这个函数:
int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for (int n : nums) sum += n;
// 这两种情况,不可能存在合法的子集划分
if (sum < target || (sum + target) % 2 == 1) {
return 0;
}
return subsets(nums, (sum + target) / 2);
}
好的,变成背包问题的标准形式:
有一个背包,容量为 sum,现在给你 N 个物品,第 i 个物品的重量为 nums[i],每个物品只有一个,请问你有几种不同的方法能够恰好装满这个背包?
现在,这就是一个正宗的动态规划问题了,下面按照我们一直强调的动态规划套路走流程:
第一步要明确两点,「状态」和「选择」。
对于背包问题,这个都是一样的,状态就是「背包的容量」和「可选择的物品」,选择就是「装进背包」或者「不装进背包」。
第二步要明确 dp 数组的定义。
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[i]种方法
其实也可以使用二维dp数组来求解本题,dp[i][j]:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种方法。
第三步确定递推公式。
有哪些来源可以推出dp[j]呢?
不考虑nums[i]的情况下,填满容量为j - nums[i]的背包,有dp[j]种方法。
那么只要搞到nums[i]的话,凑成dp[j]就有dp[j - nums[i]] 种方法。
所以求组合类问题的公式,都是类似这种:
dp[j] += dp[j - nums[i]]
然后,根据状态转移方程写出动态规划算法:
int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for (int n : nums) sum += n;
// 这两种情况,不可能存在合法的子集划分
if (sum < target || (sum + target) % 2 == 1) {
return 0;
}
return subsets(nums, (sum + target) / 2);
}
/* 计算 nums 中有几个子集的和为 sum */
int subsets(int[] nums, int sum) {
int n = nums.length;
int[] dp = new int[sum + 1];
// 初始化:什么都不放也是一种方法
dp[0] = 1;
for (int i = 0; i < n; i++) {
for (int j = sum; j >= nums[i]; j--) {
dp[j] = dp[j] + dp[j-nums[i]];
}
}
return dp[sum];
}
#501. 二叉搜索树中的众数
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#509. 斐波那契数
- easy
- 2020.11.01:😭
题目:
斐波那契数,通常用 F(n) 表示,形成的序列称为斐波那契数列。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
给定 N,计算 F(N)。
示例 1:
输入:2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1.
示例 2:
输入:3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2.
分析:
方法一:暴力递归
这个不用多说了,学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂,但是十分低效,低效在哪里?假设 n = 20,请画出递归树:
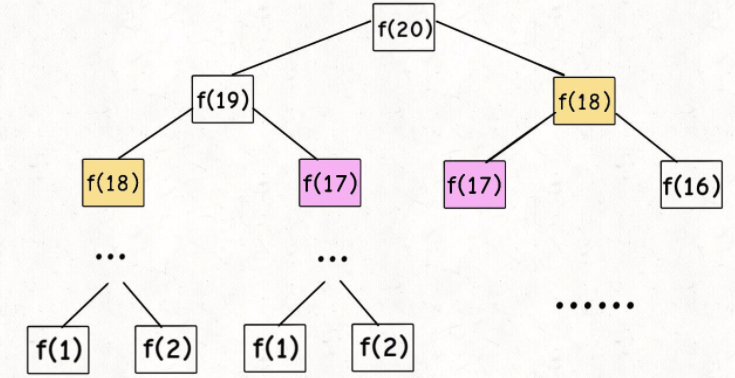
递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间。
首先计算子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2^n)。
然后计算解决一个子问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2) 一个加法操作,时间为 O(1)。
所以,这个算法的时间复杂度为二者相乘,即 O(2^n),指数级别,爆炸。
观察递归树,很明显发现了算法低效的原因:存在大量重复计算,比如 f(18) 被计算了两次,而且你可以看到,以 f(18) 为根的这个递归树体量巨大,多算一遍,会耗费巨大的时间。更何况,还不止 f(18) 这一个节点被重复计算,所以这个算法及其低效。
这就是动态规划问题的第一个性质:重叠子问题。下面,我们想办法解决这个问题。
方法二:带备忘录的递归解法
明确了问题,其实就已经把问题解决了一半。即然耗时的原因是重复计算,那么我们可以造一个「备忘录」,每次算出某个子问题的答案后别急着返回,先记到「备忘录」里再返回;每次遇到一个子问题先去「备忘录」里查一查,如果发现之前已经解决过这个问题了,直接把答案拿出来用,不要再耗时去计算了。
一般使用一个数组充当这个「备忘录」,当然你也可以使用哈希表(字典),思想都是一样的。
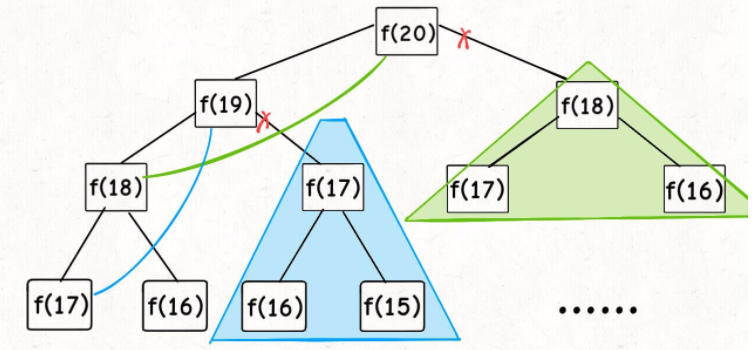
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
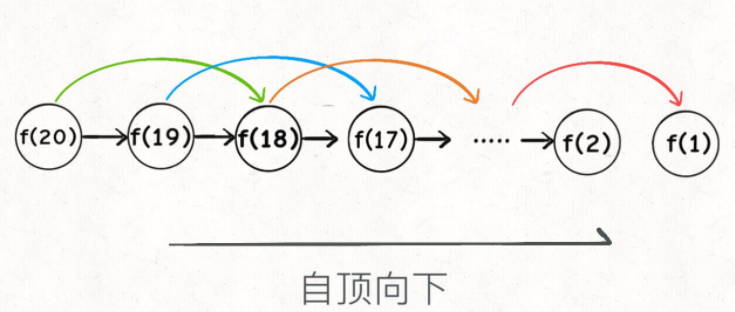
复杂度计算:
子问题个数,即图中节点的总数,由于本算法不存在冗余计算,子问题就是 f(1), f(2), f(3) … f(20),数量和输入规模 n = 20 成正比,所以子问题个数为 O(n)。
解决一个子问题的时间,同上,没有什么循环,时间为 O(1)。
所以,本算法的时间复杂度是 O(n)。比起暴力算法,是降维打击。
至此,带备忘录的递归解法的效率已经和迭代的动态规划解法一样了。实际上,这种解法和迭代的动态规划已经差不多了,只不过这种方法叫做「自顶向下」,动态规划叫做「自底向上」。
啥叫「自顶向下」?注意我们刚才画的递归树(或者说图),是从上向下延伸,都是从一个规模较大的原问题比如说 f(20),向下逐渐分解规模,直到 f(1) 和 f(2) 这两个 base case,然后逐层返回答案,这就叫「自顶向下」。
啥叫「自底向上」?反过来,我们直接从最底下,最简单,问题规模最小的 f(1) 和 f(2) 开始往上推,直到推到我们想要的答案 f(20),这就是动态规划的思路,这也是为什么动态规划一般都脱离了递归,而是由循环迭代完成计算。
⭐️ 方法三:dp 数组的迭代解法
有了上一步「备忘录」的启发,我们可以把这个「备忘录」独立出来成为一张表,就叫做 DP table 吧,在这张表上完成「自底向上」的推算岂不美哉!
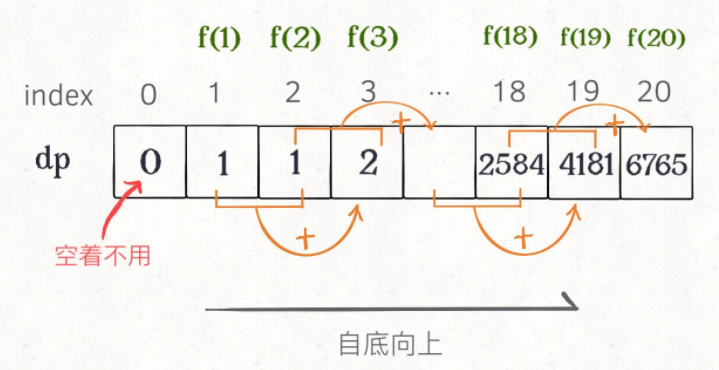
画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已。实际上,带备忘录的递归解法中的「备忘录」,最终完成后就是这个 DP table,所以说这两种解法其实是差不多的,大部分情况下,效率也基本相同。
这里,引出「状态转移方程」这个名词,实际上就是描述问题结构的数学形式:
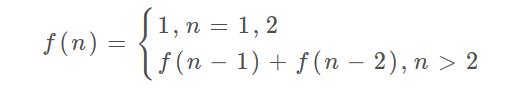
为啥叫「状态转移方程」?其实就是为了听起来高端。你把 f(n) 想做一个状态 n,这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来,这就叫状态转移,仅此而已。
你会发现,上面的几种解法中的所有操作,例如 return f(n - 1) + f(n - 2),dp[i] = dp[i - 1] + dp[i - 2],以及对备忘录或 DP table 的初始化操作,都是围绕这个方程式的不同表现形式。可见列出「状态转移方程」的重要性,它是解决问题的核心。而且很容易发现,其实状态转移方程直接代表着暴力解法。
千万不要看不起暴力解,动态规划问题最困难的就是写出这个暴力解,即状态转移方程。只要写出暴力解,优化方法无非是用备忘录或者 DP table,再无奥妙可言。
⚠️ 这个例子的最后,讲一个细节优化。细心的读者会发现,根据斐波那契数列的状态转移方程,当前状态只和之前的两个状态有关,其实并不需要那么长的一个 DP table 来存储所有的状态,只要想办法存储之前的两个状态就行了。所以,可以进一步优化,把空间复杂度降为 O(1):
这个技巧就是所谓的「状态压缩」,如果我们发现每次状态转移只需要 DP table 中的一部分,那么可以尝试用状态压缩来缩小 DP table 的大小,只记录必要的数据,上述例子就相当于把DP table 的大小从 n 缩小到 2。后续的动态规划章节中我们还会看到这样的例子,一般来说是把一个二维的 DP table 压缩成一维,即把空间复杂度从 O(n^2) 压缩到 O(n)。
代码:
// 方法一
class Solution {
public int fib(int N) {
if (N==0) return 0;
if (N==1||N==2) return 1;
return fib(N-1)+fib(N-2);
}
}
// 方法二
class Solution {
public int fib(int N) {
if (N<1) return 0;
// 备忘录全初始化为0
int[] memo = new int[N+1];
// 进行带备忘录的回归
return helper(memo,N);
}
public int helper(int[] memo,int n){
// base case
if (n==1||n==2) return 1;
// 已经计算过
if (memo[n] !=0) return memo[n];
memo[n] = helper(memo,n-1)+helper(memo,n-2);
return memo[n];
}
}
// 方法三
class Solution {
public int fib(int N) {
if (N==0) return 0;
if (N == 1) return 1;
int[] dp = new int[N+1];
// base case
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <=N ; i++) {
dp[i]=dp[i-1]+dp[i-2];
}
return dp[N];
}
}
// 再优化
// 当前状态只和之前的两个状态有关,其实并不需要那么长的一个 DP table 来存储所有的状态
class Solution {
public int fib(int N) {
if (N==0) return 0;
if (N == 2 || N == 1) return 1;
int prev = 1;
int curr = 1;
for (int i = 3; i <= N; i++) {
int sum = prev + curr;
prev = curr;
curr = sum;
}
return curr;
}
}
#513. 找树左下角的值
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#516. 最长回文子序列
- 中等
- 2021.04.13:
题目:
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = "bbbab"
输出:4
解释:一个可能的最长回文子序列为 "bbbb" 。
示例 2:
输入:s = "cbbd"
输出:2
解释:一个可能的最长回文子序列为 "bb" 。
分析:动态规划
-
状态:
dp[i][j]表示s的第i个字符到第j个字符组成的子串中,最长的回文序列长度是多少。 -
初始化:
dp[i][i] = 1单个字符的最长回文序列是 1。 j必须大于i,不满足的都初始化为0. -
转移方程:
-
如果 s 的第 i 个字符和第 j 个字符相同的话
dp[i][j] = dp[i + 1][j - 1] + 2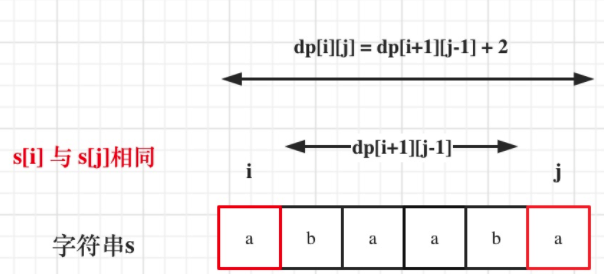
-
如果 s 的第 i 个字符和第 j 个字符不同的话
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])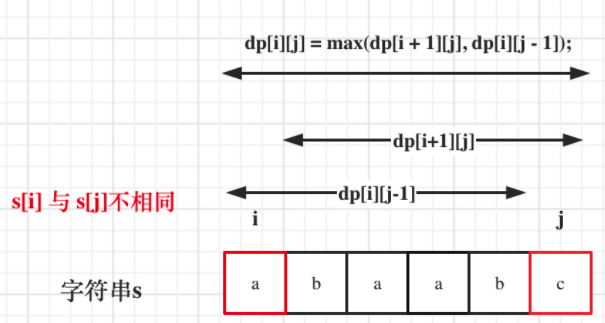
-
-
遍历顺序:
dp[i][j]是依赖于dp[i + 1][j - 1]、dp[i][j - 1]和dp[i + 1][j]。也就是从矩阵的角度来说是dp[i][j]下一行和左边的的数据。 所以遍历i的时候一定要从下到上,从左到右遍历,这样才能保证,下一行的数据是经过计算的。 -
结果:
dp[0][n - 1]
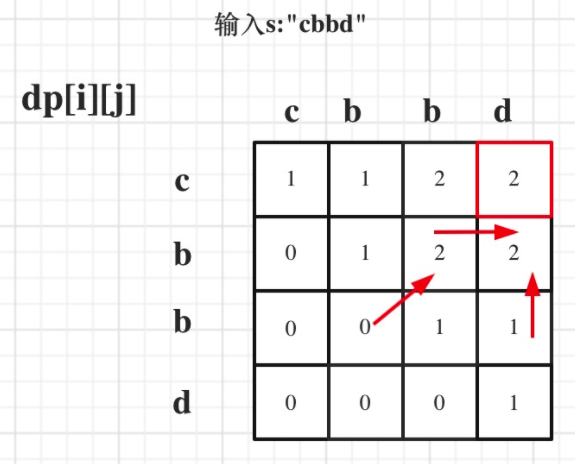
代码:
public int longestPalindromeSubseq(String s) {
int len = s.length();
int[][] dp = new int[len + 1][len + 1];
// 从后往前遍历 保证情况不漏
for (int i = len - 1; i >= 0; i--) {
dp[i][i] = 1; // 初始化
for (int j = i + 1; j < len; j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], Math.max(dp[i][j], dp[i][j - 1]));
}
}
}
return dp[0][len - 1];
}
#518. 零钱兑换 II
题目:
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
分析:
我们可以把这个问题转化为背包问题的描述形式:
有一个背包,最大容量为amount,有一系列物品coins,每个物品的重量为coins[i],每个物品的数量无限。请问有多少种方法,能够把背包恰好装满?
这个问题和我们前面讲过的两个背包问题,有一个最大的区别就是,每个物品的数量是无限的,这也就是传说中的「完全背包问题」,没啥高大上的,无非就是状态转移方程有一点变化而已。
但本题和纯完全背包不一样,纯完全背包是能否凑成总金额,而本题是要求凑成总金额的个数!
注意题目描述中是凑成总金额的硬币组合数,为什么强调是组合数呢?
例如示例一:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合,都是 2 2 1。
如果问的是排列数,那么上面就是两种排列了。组合不强调元素之间的顺序,排列强调元素之间的顺序。
dp[j]:凑成总金额j的货币组合数为dp[j]
递推公式:dp[j] += dp[j - coins[i]];
初始化:首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。从dp[i]的含义上来讲就是,凑成总金额0的货币组合数为1。
public int change(int amount, int[] coins) {
//递推表达式
int[] dp = new int[amount + 1];
//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装
dp[0] = 1;
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}
#524. 最长子序列
- easy
- 2019.09.16:😭
- 2021.03.05:😭 字典顺序指的是按顺序比较各个字母。
题目:
给定一个字符串和一个字符串字典,找到字典里面最长的字符串,该字符串可以通过删除给定字符串的某些字符来得到。如果答案不止一个,返回长度最长且字典顺序最小的字符串。如果答案不存在,则返回空字符串。
示例 1:
输入:
s = "abpcplea", d = ["ale","apple","monkey","plea"]
输出:
"apple"
说明:
所有输入的字符串只包含小写字母。
字典的大小不会超过 1000。
所有输入的字符串长度不会超过 1000。
分析:
这题的关键就是怎么在字符串字典中找到那个对应的字符串。其实很简单。
只要利用两个指针i,j,一个指向s字符串,一个指向s1字符串,每一次查找过程中,i依次后移,若i,j对应的两个字符相等,则j后移,如果j可以移到s1.length(),那么说明s1中对应的字符s中都有,即s中删除一些字符后,可以得到s1字符串,最后一步就是比较当前的结果字符与找到的s1字符,按照题目的需求来决定是否改变结果字符,是不是还挺简单的呀。
时间复杂度:O(n)
空间复杂度:O(1)
代码:
class Solution {
// s = "abpcplea", d = ["ale","apple","monkey","plea"]
public String findLongestWord(String s, List<String> d) {
// 定义连个指针,一个指向s字符串,一个指向s1
String str = "";
for (String s1 : d) {
// 每一次查找过程中,i依次后移,若i,j对应的两个字符相等,则j后移,如果j可以移到s1.length(),
// 那么说明s1中对应的字符s中都有,即s中删除一些字符后,可以得到s1字符串,
for (int i=0,j=0;i<s.length()&&j<s1.length();i++){
if (s.charAt(i)==s1.charAt(j)) j++;
if (j==s1.length()){
// 比较当前的结果字符与找到的s1字符,按照题目的需求来决定是否改变结果字符
// 找到字典里面最长的字符串;如果答案不止一个,返回长度最长且字典顺序最小的字符串
if (s1.length()>str.length()||(s1.length()==str.length()&&str.compareTo(s1)>0)){
str=s1;
}
}
}
}
return str;
}
}
#530. 二叉搜索树的最小绝对差
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#538. 把二叉搜索树转换为累加树
- Medium
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#543. 二叉树的直径
- easy
- 2020.10.14:😭
- 2021.03.17:😎 不就是左子树高度+右子树高度
题目:
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
分析:
方法一:深度优先搜索
首先我们知道一条路径的长度为该路径经过的节点数减一,所以求直径(即求路径长度的最大值)等效于求路径经过节点数的最大值减一。
而任意一条路径均可以被看作由某个节点为起点,从其左儿子和右儿子向下遍历的路径拼接得到。
如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 2 为起点,从其左儿子向下遍历的路径 [2, 4, 9] 和从其右儿子向下遍历的路径 [2, 5, 7, 8] 拼接得到。
返回直径5(两结点之间的路径长度是以它们之间边的数目表示),也可以理解为2(左子树深度) +3(右子树深度)。
-
时间复杂度:O(N),其中 N 为二叉树的节点数,即遍历一棵二叉树的时间复杂度,每个结点只被访问一次。
-
空间复杂度:O(Height),其中 Height 为二叉树的高度。由于递归函数在递归过程中需要为每一层递归函数分 配栈空间,所以这里需要额外的空间且该空间取决于递归的深度,而递归的深度显然为二叉树的高度,并且每次递归调用的函数里又只用了常数个变量,所以所需空间复杂度为 O(Height) 。
代码:
class Solution {
int max=0;
public int diameterOfBinaryTree(TreeNode root) {
depth(root);
return max;
}
public int depth(TreeNode node){
if(node==null){
return 0;
}
int Left = depth(node.left);
int Right = depth(node.right);
max=Math.max(Left+Right,max);//将每个节点最大直径(左子树深度+右子树深度)当前最大值比较并取大者
return Math.max(Left,Right)+1;//返回节点深度
}
}
#567. 字符串的排列
- 中等
- 2020.12.02:😭
- 2021.03.06:😎
题目:
给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列。
换句话说,第一个字符串的排列之一是第二个字符串的子串。
示例1:
输入: s1 = "ab" s2 = "eidbaooo"
输出: True
解释: s2 包含 s1 的排列之一 ("ba").
注意:
输入的字符串只包含小写字母
两个字符串的长度都在 [1, 10,000] 之间
分析:
注意哦,输入的 s1 是可以包含重复字符的,所以这个题难度不小。
这种题目,是明显的滑动窗口算法,相当给你一个 S 和一个 T,请问你 S 中是否存在一个子串,包含 T 中所有字符且不包含其他字符?
首先,先复制粘贴之前的算法框架代码,然后明确刚才提出的 4 个问题,即可写出这道题的答案:
public boolean checkInclusion(String s1, String s2) {
// need 和 window 散列表 初始化need
HashMap<Character, Integer> need = new HashMap<>();
for (char key : s1.toCharArray()) {
need.put(key, need.getOrDefault(key, 0) + 1);
}
HashMap<Character, Integer> window = new HashMap<>();
// 滑动窗口指针 left/right 统计参数valid
int left = 0;
int right = 0;
int valid = 0;
// 开始滑动
char[] sArray = s2.toCharArray();
while (right < sArray.length) {
// right 增加
Character c = sArray[right];
right++;
// 进行一系列的更新
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
// 更新valid
if (window.get(c).equals(need.get(c))) {
valid++;
}
}
// 缩小窗口的时机: 窗口大小>=s1.length,因为排列必须保持长度一致
while ((right - left) >= s1.length()) {
// 当发现 valid == need.size() 时,就说明窗口中就是一个合法的排列,所以立即返回 true
// 注意 need.size()和s1.length() 是不相等的,因为s1中可能有重复字符
if (valid == need.size()) return true;
Character d = sArray[left];
left++;
// 进行一系列的更新
if (need.containsKey(d)) {
// 更新valid
if (window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.get(d) - 1);
}
}
}
return false; //未找到子串
}
对于这道题的解法代码,基本上和最小覆盖子串一模一样,只需要改变两个地方:
1、本题移动 left 缩小窗口的时机是窗口大小大于等于 t.size() 时,应为排列嘛,显然长度应该是一样的。
2、当发现 valid == need.size() 时,就说明窗口中就是一个合法的排列,所以立即返回 true。
至于如何处理窗口的扩大和缩小,和最小覆盖子串完全相同。
#572. 另一个树的子树
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#583. 两个字符串的删除操作
- 中等
- 2020.12.02:😭
题目:
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
示例:
输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
提示:
给定单词的长度不超过500。
给定单词中的字符只含有小写字母。
分析:
题目让我们计算将两个字符串变得相同的最少删除次数,那我们可以思考一下,最后这两个字符串会被删成什么样子?
删除的结果不就是它俩的最长公共子序列嘛!
那么,要计算删除的次数,就可以通过最长公共子序列的长度推导出来:
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int lcs = longestCommonSubsequence(word1,word2,m,n);
return m-lcs+n-lcs;
}
public int longestCommonSubsequence(String s1,String s2,int m,int n){
int[][] dp = new int[m+1][n+1];
for (int i = 1; i <=m; i++) {
for (int j = 1; j <=n; j++) {
if (s1.charAt(i-1)==s2.charAt(j-1)){
dp[i][j]= dp[i-1][j-1]+1;
}else {
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[m][n];
}
这道题就解决了!
#617. 合并二叉树
- easy
- 2020.10.01:😭
题目:
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
分析:
需要注意:这两颗树并不是长得完全一样,有的树可能有左节点,但有的树没有。 对于这种情况,我们统一的都把他们挂到树 1 上面就可以了,对于上面例子中的两颗树,合并起来的结果如下:
3
/ \
4 5
/ \ \
5 4 7 **相当于树1少了一条腿,而树 2 有这条腿,那就把树 2 的拷贝过来。** 总结下递归的条件:
终止条件:树 1 的节点为 null,或者树 2 的节点为 null 递归函数内:将两个树的节点相加后,再赋给树 1 的节点。再递归的执行两个树的左节点,递归执行两个树的右节点
代码:
class Solution {
public TreeNode mergeTrees(TreeNode r1, TreeNode r2) {
// 如果 r1和r2中,只要有一个是null,函数就直接返回
if(r1==null || r2==null) {
return r1==null? r2 : r1;
}
//让r1的值 等于 r1和r2的值累加,再递归的计算两颗树的左节点、右节点
r1.val += r2.val;
r1.left = mergeTrees(r1.left,r2.left);
r1.right = mergeTrees(r1.right,r2.right);
return r1;
}
}
#633. 两数平方和
- Easy
- 2019.09.10:😭
- 2019.09.11:😎
- 2021.03.05:😎
题目:
给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 + b2 = c。
示例1:
输入: 5
输出: True
解释: 1 * 1 + 2 * 2 = 5
分析:
方法一:双指针
判断c是否为非负整数,若是,则直接返回false
利用Math包中sqrt()方法求出小于c的平方根的最大整数作为右指针,同时设置左指针从0开始;
开始循环,若左指针小于右指针,判断两指针之和与c的大小;
若和等于c,返回false;
若和小于c,左指针加1;
若和大于c,右指针减1;
默认返回false
复杂度分析:
时间复杂度O(sqrt(c))
空间复杂度O(1)
代码:
// 双指针
class Solution {
public boolean judgeSquareSum(int c) {
if (c<0) return false;
int i = 0; //双指针的左指针
int j = (int) Math.sqrt(c); //双指针的右指针
while (i<=j){
long sum = i*i+j*j; // 防止 sum变量溢出
if (sum==c) return true;
else if (sum<c){
i++;
}else{j--;}
}
return false;
}
}
#637. 二叉树的层平均值
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#647. 回文子串
- 中等
- 2021.04.11:😎
题目:
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:"abc"
输出:3
解释:三个回文子串: "a", "b", "c"
示例 2:
输入:"aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
分析:
方法一:中心扩展
寻找回文串的问题核心思想是:从中间开始向两边扩散来判断回文串。对于最长回文子串,就是这个意思:
for 0 <= i < len(s):
找到以 s[i] 为中心的回文串
更新答案
但是呢,我们刚才也说了,回文串的长度可能是奇数也可能是偶数,如果是abba这种情况,没有一个中心字符,上面的算法就没辙了。所以我们可以修改一下:
for 0 <= i < len(s):
找到以 s[i] 为中心的回文串
找到以 s[i] 和 s[i+1] 为中心的回文串
更新答案
注意防止越界。
方法二:动态规划
状态:dp[i][j] 表示字符串s在[i,j]区间的子串是否是一个回文串。
状态转移方程:当 s[i] == s[j] && (j - i < 2 || dp[i + 1][j - 1]) 时,dp[i][j]=true,否则为false
这个状态转移方程是什么意思呢?
- case1: 当只有一个字符时,比如 a 自然是一个回文串。
- case2: 当有两个字符时,如果是相等的,比如 aa,也是一个回文串。
- case3: 当有三个及以上字符时,比如 ababa 这个字符记作串 1,把两边的 a 去掉,也就是 bab 记作串 2,可以看出只要串2是一个回文串,那么左右各多了一个 a 的串 1 必定也是回文串。所以当
s[i]==s[j]时,自然要看dp[i+1][j-1]是不是一个回文串。

遍历顺序:
s[i]==s[j]取决于状态 dp[i+1][j-1] 。
所以遍历顺序需要从下到上(i),从左到右(j)。
代码:
// 方法一:中心扩展
private int res=0;
public int countSubstrings(String s) {
for (int i = 0; i < s.length(); i++) {
isPalindrome(s,i,i);
isPalindrome(s,i,i+1);
}
return res;
}
// 判断时候是回文串,注意防止越界
private void isPalindrome(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)){
left--;
right++;
res++;
}
}
// 方法二 动态规划
public int countSubstrings(String s) {
boolean[][] dp = new boolean[s.length()][s.length()];
int ans = 0;
for (int i = s.length() - 1; i >= 0; i--) { // 注意遍历顺序
for (int j = i; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1])) {
dp[i][j] = true;
ans++;
}
}
}
return ans;
}
// 可读性高一点的写法
public int countSubstrings(String s) {
boolean[][] dp = new boolean[s.length()][s.length()];
int ans = 0;
// 注意遍历顺序
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j)) {
if (j - i < 2) { // case1 和 case2
ans++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // case3
ans++;
dp[i][j] = true;
}
}
}
}
return ans;
}
#652. 寻找重复的子树
- 中等
- 2020.10.01:😭
题目:
给定一棵二叉树,返回所有重复的子树。对于同一类的重复子树,你只需要返回其中任意一棵的根结点即可。
两棵树重复是指它们具有相同的结构以及相同的结点值。
示例 1:
1
/ \
2 3
/ / \
4 2 4
/
4
下面是两个重复的子树:
2
/
4
和
4
因此,你需要以列表的形式返回上述重复子树的根结点。
分析:
这题咋做呢?还是老套路,先思考,对于某一个节点,它应该做什么。
比如说,你站在图中这个节点 2 上:
如果你想知道以自己为根的子树是不是重复的,是否应该被加入结果列表中,你需要知道什么信息?
你需要知道以下两点:
1、以我为根的这棵二叉树(子树)长啥样?
2、以其他节点为根的子树都长啥样?
这就叫知己知彼嘛,我得知道自己长啥样,还得知道别人长啥样,然后才能知道有没有人跟我重复,对不对?
好,那我们一个一个来看,先来思考,我如何才能知道以自己为根的二叉树长啥样?
其实看到这个问题,就可以判断本题要使用「后序遍历」框架来解决:
void traverse(TreeNode root) {
traverse(root.left);
traverse(root.right);
/* 解法代码的位置 */
}
为什么?很简单呀,我要知道以自己为根的子树长啥样,是不是得先知道我的左右子树长啥样,再加上自己,就构成了整棵子树的样子?
所以,我们可以通过拼接字符串的方式把二叉树序列化,看下代码:
String traverse(TreeNode root) {
// 对于空节点,可以用一个特殊字符表示
if (root == null) {
return "#";
}
// 将左右子树序列化成字符串
String left = traverse(root.left);
String right = traverse(root.right);
/* 后序遍历代码位置 */
// 左右子树加上自己,就是以自己为根的二叉树序列化结果
String subTree = left + "," + right + "," + root.val;
return subTree;
}
我们用非数字的特殊符 # 表示空指针,并且用字符 , 分隔每个二叉树节点值,这属于序列化二叉树的套路了,不多说。
注意我们 subTree 是按照左子树、右子树、根节点这样的顺序拼接字符串,也就是后序遍历顺序。你完全可以按照前序或者中序的顺序拼接字符串,因为这里只是为了描述一棵二叉树的样子,什么顺序不重要。
这样,我们第一个问题就解决了,对于每个节点,递归函数中的 subTree 变量就可以描述以该节点为根的二叉树。
现在我们解决第二个问题,我知道了自己长啥样,怎么知道别人长啥样?这样我才能知道有没有其他子树跟我重复对吧。
这很简单呀,我们借助一个外部数据结构,让每个节点把自己子树的序列化结果存进去,这样,对于每个节点,不就可以知道有没有其他节点的子树和自己重复了么?
初步思路可以使用 HashMap,额外记录每棵子树的出现次数,代码如下:
// 记录所有子树以及出现的次数
HashMap<String, Integer> memo = new HashMap<>();
// 记录重复的子树根节点
LinkedList<TreeNode> res = new LinkedList<>();
/* 主函数 */
List<TreeNode> findDuplicateSubtrees(TreeNode root) {
traverse(root);
return res;
}
/* 辅助函数 */
String traverse(TreeNode root) {
if (root == null) {
return "#";
}
String left = traverse(root.left);
String right = traverse(root.right);
String subTree = left + "," + right+ "," + root.val;
int freq = memo.getOrDefault(subTree, 0);
// 多次重复也只会被加入结果集一次
if (freq == 1) {
res.add(root);
}
// 给子树对应的出现次数加一
memo.put(subTree, freq + 1);
return subTree;
}
代码:
class Solution {
// 记录所有子树以及出现的次数
HashMap<String, Integer> memo = new HashMap<>();
// 记录重复的子树根节点
LinkedList<TreeNode> res = new LinkedList<>();
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
traverse(root);
return res;
}
/* 辅助函数 */
public String traverse(TreeNode root){
// 对于空节点,可以用一个特殊字符表示
if (root==null) return "#";
// 将左右子树序列化成字符串
String left = traverse(root.left);
String right = traverse(root.right);
/* 后序遍历代码位置 */
// 左右子树加上自己,就是以自己为根的二叉树序列化结果
String subTree=left + "," + right + "," + root.val; // 描述以该节点为根的二叉树。
int freq = memo.getOrDefault(subTree,0);
// 多次重复也只会被加入结果集一次
if (freq==1) res.add(root);
// 对子树对应的出现次数加1
memo.put(subTree,freq+1);
return subTree;
}
}
#653. 两数之和 IV - 输入 BST
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#654. 最大二叉树
- 中等
- 2020.10.01:😭
- 2020.10.21:😎
- 2020.11.01:😎
题目:
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
二叉树的根是数组中的最大元素。
左子树是通过数组中最大值左边部分构造出的最大二叉树。
右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树,并且输出这个树的根节点。
示例 :
输入:[3,2,1,6,0,5]
输出:返回下面这棵树的根节点:
6
/ \
3 5
\ /
2 0
\
1
分析:
按照我们刚才说的,先明确根节点做什么?对于构造二叉树的问题,根节点要做的就是把想办法把自己构造出来。
我们肯定要遍历数组把找到最大值maxVal,把根节点root做出来,然后对maxVal左边的数组和右边的数组进行递归调用,作为root的左右子树。
按照题目给出的例子,输入的数组为[3,2,1,6,0,5],对于整棵树的根节点来说,其实在做这件事:
TreeNode constructMaximumBinaryTree([3,2,1,6,0,5]) {
// 找到数组中的最大值
TreeNode root = new TreeNode(6);
// 递归调用构造左右子树
root.left = constructMaximumBinaryTree([3,2,1]);
root.right = constructMaximumBinaryTree([0,5]);
return root;
}
再详细一点,就是如下伪码:
TreeNode constructMaximumBinaryTree(int[] nums) {
if (nums is empty) return null;
// 找到数组中的最大值
int maxVal = Integer.MIN_VALUE;
int index = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] > maxVal) {
maxVal = nums[i];
index = i;
}
}
TreeNode root = new TreeNode(maxVal);
// 递归调用构造左右子树
root.left = constructMaximumBinaryTree(nums[0..index-1]);
root.right = constructMaximumBinaryTree(nums[index+1..nums.length-1]);
return root;
}
看懂了吗?对于每个根节点,只需要找到当前nums中的最大值和对应的索引,然后递归调用左右数组构造左右子树即可。
代码:
public TreeNode constructMaximumBinaryTree(int[] nums) {
return build(nums,0,nums.length-1);
}
// 先序遍历创建根节点,将 nums[lo..hi] 构造成符合条件的树
public TreeNode build(int[] nums,int low,int high){
if (low>high) return null;
// 找到数组中的最大值和对应的索引
int index = getMaxIndex(nums,low,high);
TreeNode root = new TreeNode(nums[index]);
// 递归调用构造左右子树
root.left = build(nums,low,index-1);
root.right = build(nums,index+1,high);
return root;
}
public int getMaxIndex(int[] nums,int left,int right){
int max = Integer.MIN_VALUE;
int index = -1;
for(int i = left;i<=right;i++){
if(nums[i]>max){
max = nums[i];
index = i;
}
}
return index;
}
#669. 修剪二叉搜索树
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#674. 最长连续递增序列
- Easy
- 2019.08.30:😭
题目:
给定一个未经排序的整数数组,找到最长且连续的的递增序列,并返回该序列的长度。
示例 1:
输入: [1,3,5,4,7]
输出: 3
解释: 最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为5和7在原数组里被4隔开。
注意:数组长度不会超过10000。
分析:动态规划
算法:
每个(连续)增加的子序列是不相交的,并且每当 nums[i-1]>=nums[i] 时,每个此类子序列的边界都会出现。当它这样做时,它标志着在 nums[i] 处开始一个新的递增子序列,我们将这样的 i 存储在变量 anchor 中。
例如,如果 nums=[7,8,9,1,2,3],那么 anchor 从 0 开始(nums[anchor]=7),并再次设置为 anchor=3(nums[anchor]=1)。无论 anchor 的值如何,我们都会记录 i-anchor+1 的候选答案、子数组 nums[anchor]、nums[anchor+1]、…、nums[i] 的长度,并且我们的答案会得到适当的更新。
复杂度分析:
时间复杂度:O(N)O(N),其中 NN 是 nums 的长度。我们通过 nums 执行一个循环。
空间复杂度:O(1)O(1),anchor 和 ans 使用了常数级空间。
代码:
class Solution {
public int findLengthOfLCIS(int[] nums) {
// nums[anchor] 处开始一个新的递增子序列
// ans 当前子序列长度
int ans = 0, anchor = 0;
for (int i = 0; i < nums.length; i++) {
// i=0时候,i>0为false就不会继续操作&&后的代码了
if (i > 0 && nums[i-1] >= nums[i]) anchor = i;
ans = Math.max(ans, i - anchor + 1);
}
return ans;
}
}
#671. 二叉树中第二小的节点
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#677. 键值映射
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#680. 回文字符串
- Easy
- 2019.09.12:😭
- 2019.10.13:😎
- 2021.03.05:😎
题目:
给定一个非空字符串 s,最多删除一个字符。判断是否能成为回文字符串。
示例 1:
输入: "aba"
输出: True
示例 2:
输入: "abca"
输出: True
解释: 你可以删除c字符。
分析:
方法一:双指针(简单易懂)
所谓的回文字符串,是指具有左右对称特点的字符串,例如 "abcba" 就是一个回文字符串。
使用双指针可以很容易判断一个字符串是否是回文字符串:令一个指针从左到右遍历,一个指针从右到左遍历,这两个指针同时移动一个位置,每次都判断两个指针指向的字符是否相同,如果都相同,字符串才是具有左右对称性质的回文字符串。
本题的关键是处理删除一个字符。在使用双指针遍历字符串时,如果出现两个指针指向的字符不相等的情况,我们就试着删除一个字符,再判断删除完之后的字符串是否是回文字符串。
在判断是否为回文字符串时,我们不需要判断整个字符串,因为左指针左边和右指针右边的字符之前已经判断过具有对称性质,所以只需要判断中间的子字符串即可。
在试着删除字符时,我们既可以删除左指针指向的字符,也可以删除右指针指向的字符。
复杂度分析:
时间复杂度O(n),空间复杂度如果忽略递归的压栈信息,O(1)
方法二:贪心算法
代码:
// 方法一:
class Solution {
public boolean validPalindrome(String s) {
// 最多删除一个字符
// 在遇到不同的时候,移除一个元素(左/右)
int i = 0;
int j = s.length()-1;
while(i<j){
if (s.charAt(i)!=s.charAt(j)){
// 在试着删除字符时,我们既可以删除左指针指向的字符(左边加一),也可以删除右指针指向的字符(右边减一)
return isPalindrome(s,i,j-1)||isPalindrome(s,i+1,j);
}
i++;
j--;
}
return true;
}
// 判断是否是回文字符串
// 在判断是否为回文字符串时,我们不需要判断整个字符串,因为左指针左边和右指针右边的字符之前已经判断过具有对称性质,所以只需要判断中间的子字符串即可
public boolean isPalindrome(String s, int i, int j) {
while (i < j) {
if (s.charAt(i++) != s.charAt(j--)) {
return false;
}
}
return true;
}
}
#687. 最长同值路径
- easy
- 2020.10.01:😭
题目:
分析:
方法一:递归
- 时间复杂度:O()
- 空间复杂度:O()
代码:
#704. 二分查找
- 简单
- 2020.11.25:😭
题目:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
分析:
#712. 两个字符串的最小ASCII删除和
- 中等
- 2020.12.02:😭
题目:
给定两个字符串s1, s2,找到使两个字符串相等所需删除字符的ASCII值的最小和。
示例 1:
输入: s1 = "sea", s2 = "eat"
输出: 231
解释: 在 "sea" 中删除 "s" 并将 "s" 的值(115)加入总和。
在 "eat" 中删除 "t" 并将 116 加入总和。
结束时,两个字符串相等,115 + 116 = 231 就是符合条件的最小和。
示例 2:
输入: s1 = "delete", s2 = "leet"
输出: 403
解释: 在 "delete" 中删除 "dee" 字符串变成 "let",
将 100[d]+101[e]+101[e] 加入总和。在 "leet" 中删除 "e" 将 101[e] 加入总和。
结束时,两个字符串都等于 "let",结果即为 100+101+101+101 = 403 。
如果改为将两个字符串转换为 "lee" 或 "eet",我们会得到 433 或 417 的结果,比答案更大。
注意:
0 < s1.length, s2.length <= 1000。
所有字符串中的字符ASCII值在[97, 122]之间。
分析:
base case 有一定区别,计算lcs长度时,如果一个字符串为空,那么lcs长度必然是 0;但是这道题如果一个字符串为空,另一个字符串必然要被全部删除,所以需要计算另一个字符串所有字符的 ASCII 码之和。
关于状态转移,当s1[i]和s2[j]相同时不需要删除,不同时需要删除,所以可以利用dp函数计算两种情况,得出最优的结果。其他的大同小异。

public int minimumDeleteSum(String s1, String s2) {
int m = s1.length();
int n = s2.length();
int[][] dp = new int[m+1][n+1];
// base case
for (int i = 1; i <=n; i++) {
dp[0][i] = s2.charAt(i-1)+dp[0][i-1];
}
for (int i = 1; i <=m; i++) {
dp[i][0] = s1.charAt(i-1)+dp[i-1][0];
}
for (int i = 1; i <=m ; i++) {
for (int j = 1; j <= n; j++) {
if (s1.charAt(i-1)==s2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}else {
dp[i][j] = Math.min(s2.charAt(j-1)+dp[i][j - 1], s1.charAt(i-1)+dp[i - 1][j]);
}
}
}
return dp[m][n];
}
#752. 打开转盘锁
- 中等
- 2020.11.25:😭
题目:
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出最小的旋转次数,如果无论如何不能解锁,返回 -1。
示例 1:
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,
因为当拨动到 "0102" 时这个锁就会被锁定。
分析:
方法一:BFS
题目中描述的就是我们生活中常见的那种密码锁,若果没有任何约束,最少的拨动次数很好算,就像我们平时开密码锁那样直奔密码拨就行了。
但现在的难点就在于,不能出现 deadends,应该如何计算出最少的转动次数呢?
第一步,我们不管所有的限制条件,不管 deadends 和 target 的限制,就思考一个问题:如果让你设计一个算法,穷举所有可能的密码组合,你怎么做?
穷举呗,再简单一点,如果你只转一下锁,有几种可能?总共有 4 个位置,每个位置可以向上转,也可以向下转,也就是有 8 种可能对吧。
比如说从 "0000" 开始,转一次,可以穷举出 "1000", "9000", "0100", "0900"... 共 8 种密码。然后,再以这 8 种密码作为基础,对每个密码再转一下,穷举出所有可能…
⭐️ 仔细想想,这就可以抽象成一幅图,每个节点有 8 个相邻的节点,又让你求最短距离,这不就是典型的 BFS 嘛,框架就可以派上用场了,先写出一个「简陋」的 BFS 框架代码再说别的:
// BFS 框架,打印出所有可能的密码
public int openLock(String[] deadends, String target) {
LinkedList<String> q = new LinkedList<>();
q.offer("0000");
// 步数
int step = 0;
while(!q.isEmpty()){
int size = q.size();
for (int i = 0; i < size; i++) {
String cur = q.poll();
// 判断是否到终点
System.out.println(cur);
// 将一个节点的相邻节点加入队列
for (int j = 0; j < 4; j++) {
String up=plusOne(cur,j);
String down=minusOne(cur,j);
q.offer(up);
q.offer(down);
}
}
// 增加步数
step++;
}
return step;
}
// 将 s[j] 向上拨动一次
private String plusOne(String s, int j) {
char[] chars = s.toCharArray();
if (chars[j]=='9'){ chars[j]='0';}else {chars[j]+=1;}
return new String(chars);
}
// 将 s[i] 向下拨动一次
private String minusOne(String s, int j) {
char[] chars = s.toCharArray();
if (chars[j]=='0'){ chars[j]='9';}else {chars[j]-=1;}
return new String(chars);
}
PS:这段代码当然有很多问题,但是我们做算法题肯定不是一蹴而就的,而是从简陋到完美的。不要完美主义,咱要慢慢来,好不。
这段 BFS 代码已经能够穷举所有可能的密码组合了,但是显然不能完成题目,有如下问题需要解决:
1、会走回头路。比如说我们从 "0000" 拨到 "1000",但是等从队列拿出 "1000" 时,还会拨出一个 "0000",这样的话会产生死循环。
2、没有终止条件,按照题目要求,我们找到 target 就应该结束并返回拨动的次数。
3、没有对 deadends 的处理,按道理这些「死亡密码」是不能出现的,也就是说你遇到这些密码的时候需要跳过。
如果你能够看懂上面那段代码,真得给你鼓掌,只要按照 BFS 框架在对应的位置稍作修改即可修复这些问题:
class Solution {
// BFS 框架,打印出所有可能的密码
public int openLock(String[] deadends, String target) {
// 记录需要跳过的死亡密码
HashSet<String> deads = new HashSet<>();
for (String deadend : deadends) {
deads.add(deadend);
}
// 记录已经穷举过的密码,防止走回头路
HashSet<String> visited = new HashSet<>();
// 从起点开始启动广度优先搜索
LinkedList<String> q = new LinkedList<>();
q.offer("0000");
visited.add("0000");
// 步数
int step = 0;
while(!q.isEmpty()){
int size = q.size();
for (int i = 0; i < size; i++) {
String cur = q.poll();
// 判断是否到终点
if (deads.contains(cur)) continue;
if (cur.equals(target)) return step;
// 将一个节点的相邻节点加入队列
for (int j = 0; j < 4; j++) {
String up=plusOne(cur,j);
if (!visited.contains(up)){
q.offer(up);
visited.add(up);
}
String down=minusOne(cur,j);
if (!visited.contains(down)){
q.offer(down);
visited.add(down);
}
}
}
// 增加步数
step++;
}
// 如果穷举完都没找到目标密码,那就是找不到了
return -1;
}
// 将 s[j] 向上拨动一次
private String plusOne(String s, int j) {
char[] chars = s.toCharArray();
if (chars[j]=='9'){ chars[j]='0';}else {chars[j]+=1;}
return new String(chars);
}
// 将 s[i] 向下拨动一次
private String minusOne(String s, int j) {
char[] chars = s.toCharArray();
if (chars[j]=='0'){ chars[j]='9';}else {chars[j]-=1;}
return new String(chars);
}
}
至此,我们就解决这道题目了。有一个比较小的优化:可以不需要 dead 这个哈希集合,可以直接将这些元素初始化到 visited 集合中,效果是一样的,可能更加优雅一些。
方法二:双向 BFS 优化
你以为到这里 BFS 算法就结束了?恰恰相反。BFS 算法还有一种稍微高级一点的优化思路:双向 BFS,可以进一步提高算法的效率。
篇幅所限,这里就提一下区别:传统的 BFS 框架就是从起点开始向四周扩散,遇到终点时停止;而双向 BFS 则是从起点和终点同时开始扩散,当两边有交集的时候停止。
为什么这样能够能够提升效率呢?其实从 Big O 表示法分析算法复杂度的话,它俩的最坏复杂度都是 O(N),但是实际上双向 BFS 确实会快一些,我给你画两张图看一眼就明白了:
图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到 target;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。从这个例子可以直观地感受到,双向 BFS 是要比传统 BFS 高效的。
不过,双向 BFS 也有局限,因为你必须知道终点在哪里。比如我们刚才讨论的二叉树最小高度的问题,你一开始根本就不知道终点在哪里,也就无法使用双向 BFS;但是第二个密码锁的问题,是可以使用双向 BFS 算法来提高效率的,代码稍加修改即可:
public int openLock(String[] deadends, String target) {
HashSet<String> deads = new HashSet<>();
for (String s : deadends) {
deads.add(s);
}
// 用集合不用队列,可以快速判断元素是否存在
HashSet<String> q1 = new HashSet<>();
HashSet<String> q2 = new HashSet<>();
HashSet<String> visited = new HashSet<>();
int step = 0;
q1.add("0000");
q2.add(target);
while (!q1.isEmpty()&&!q2.isEmpty()){
// 哈希集合在遍历的过程中不能修改,用 temp 存储扩散结果
HashSet<String> temp = new HashSet<>();
/* 将 q1 中的所有节点向周围扩散 */
for (String cur : q1) {
/* 判断是否到达终点 */
if (deads.contains(cur))
continue;
if (q2.contains(cur))
return step;
visited.add(cur);
/* 将一个节点的未遍历相邻节点加入集合 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up))
temp.add(up);
String down = minusOne(cur, j);
if (!visited.contains(down))
temp.add(down);
}
}
/* 在这里增加步数 */
step++;
// temp 相当于 q1
// 这里交换 q1 q2,下一轮 while 就是扩散 q2
q1 = q2;
q2 = temp;
}
return -1;
}
双向 BFS 还是遵循 BFS 算法框架的,只是不再使用队列,而是使用 HashSet 方便快速判断两个集合是否有交集。
另外的一个技巧点就是 while 循环的最后交换 q1 和 q2 的内容,所以只要默认扩散 q1 就相当于轮流扩散 q1 和 q2。
其实双向 BFS 还有一个优化,就是在 while 循环开始时做一个判断:
// ...
while (!q1.isEmpty() && !q2.isEmpty()) {
if (q1.size() > q2.size()) {
// 交换 q1 和 q2
temp = q1;
q1 = q2;
q2 = temp;
}
// ...
为什么这是一个优化呢?
因为按照 BFS 的逻辑,队列(集合)中的元素越多,扩散之后新的队列(集合)中的元素就越多;在双向 BFS 算法中,如果我们每次都选择一个较小的集合进行扩散,那么占用的空间增长速度就会慢一些,效率就会高一些。
不过话说回来,无论传统 BFS 还是双向 BFS,无论做不做优化,从 Big O 衡量标准来看,时间复杂度都是一样的,只能说双向 BFS 是一种 trick,算法运行的速度会相对快一点,掌握不掌握其实都无所谓。最关键的是把 BFS 通用框架记下来,反正所有 BFS 算法都可以用它套出解法。
876. 链表的中间结点
- 简单
- 2021.11.12:😎
题目:
给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
示例 1:
输入:[1,2,3,4,5]
输出:此列表中的结点 3 (序列化形式:[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意,我们返回了一个 ListNode 类型的对象 ans,这样:
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例 2:
输入:[1,2,3,4,5,6]
输出:此列表中的结点 4 (序列化形式:[4,5,6])
由于该列表有两个中间结点,值分别为 3 和 4,我们返回第二个结点。
分析:
方法一:快慢指针
注意链表为偶数的情况。
代码:
public ListNode middleNode(ListNode head) {
// 快慢指针找中点
ListNode quick = head;
ListNode slow = head;
while(quick.next!=null&&quick.next.next!=null){
slow = slow.next;
quick = quick.next.next;
}
return quick.next==null?slow:slow.next;
}
#1051. 高度检查器
- Easy
- 2019.08.28:😭 在对比一次后,忘记加arr[j]–;
- 2019.08.29:😎
题目:
学校在拍年度纪念照时,一般要求学生按照 非递减 的高度顺序排列。
请你返回能让所有学生以 非递减 高度排列的最小必要移动人数。
注意,当一组学生被选中时,他们之间可以以任何可能的方式重新排序,而未被选中的学生应该保持不动。
提示:1 <= heights.length <= 100
1 <= heights[i] <= 100
分析:桶排序
非递减 排序也就是升序排列,最直观的一种解法就是排序后对比计数每个位置的不同数量。
但是涉及到比较排序,时间复杂度最低也有 O(NlogN)O(NlogN)。
我们真的需要排序吗?
首先我们其实并不关心排序后得到的结果,我们想知道的只是在该位置上,与最小的值是否一致
题目中已经明确了值的范围 1 <= heights[i] <= 100
这是一个在固定范围内的输入,比如输入: [1,1,4,2,1,3]
输入中有 3 个 1,1 个 2,1 个 3 和 1 个 4, 3 个 1 肯定会在前面,依次类推
所以,我们需要的仅仅只是计数而已
代码:
public int heightChecker(int[] heights) {
//1 设置100个桶,用于放入身高
// 值的范围是1 <= heights[i] <= 100,因此需要1,2,3,...,99,100,共101个桶,0号桶不用
int[] arr = new int[101];
// 遍历数组heights,计算每个桶中有多少个元素,也就是数组heights中有多少个1,多少个2,...
for (int i = 0; i < heights.length; i++) {
arr[heights[i]]++;
}
//2 排序按桶的顺序依次取出(将这101个桶中的元素顺序桶地取出来,元素就是有序的),与原数组做对比
int j = 1;
int count = 0;
// 每个height必须比到一个非0值
for (int height : heights) {
while (arr[j] <= 0) {
j++;
}
if (height != j) count++;
// 2019.08.28:😭 匹配到非0值后需要移除一个桶元素
arr[j]--;
}
return count;
}
#1143. 最长公共子序列
- 中等
- 2020.12.02:😭
题目:
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
分析:
一个最简单的暴力算法就是,把s1和s2的所有子序列都穷举出来,然后看看有没有公共的,然后在所有公共子序列里面再寻找一个长度最大的。
显然,这种思路的复杂度非常高,你要穷举出所有子序列,这个复杂度就是指数级的,肯定不实际。
正确的思路是不要考虑整个字符串,而是细化到s1和s2的每个字符。前文 子序列解题模板 中总结的一个规律:
对于两个字符串求子序列的问题,都是用两个指针i和j分别在两个字符串上移动,大概率是动态规划思路。
最长公共子序列的问题也可以遵循这个规律,我们可以先写一个dp函数:
// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j)
这个dp函数的定义是:dp(s1, i, s2, j)计算s1[i..]和s2[j..]的最长公共子序列长度。
根据这个定义,那么我们想要的答案就是dp(s1, 0, s2, 0),且 base case 就是i == len(s1)或j == len(s2)时,因为这时候s1[i..]或s2[j..]就相当于空串了,最长公共子序列的长度显然是 0:
int longestCommonSubsequence(String s1, String s2) {
return dp(s1, 0, s2, 0);
}
/* 主函数 */
int dp(String s1, int i, String s2, int j) {
// base case
if (i == s1.length() || j == s2.length()) {
return 0;
}
// ...
接下来,咱不要看s1和s2两个字符串,而是要具体到每一个字符,思考每个字符该做什么。

我们只看s1[i]和s2[j],如果s1[i] == s2[j],说明这个字符一定在lcs中:

这样,就找到了一个lcs中的字符,根据dp函数的定义,我们可以完善一下代码:
// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
if (s1.charAt(i) == s2.charAt(j)) {
// s1[i] 和 s2[j] 必然在 lcs 中,
// 加上 s1[i+1..] 和 s2[j+1..] 中的 lcs 长度,就是答案
return 1 + dp(s1, i + 1, s2, j + 1)
} else {
// ...
}
}
刚才说的s1[i] == s2[j]的情况,但如果s1[i] != s2[j],应该怎么办呢?
s1[i] != s2[j]意味着,s1[i]和s2[j]中至少有一个字符不在lcs中:

如上图,总共可能有三种情况,我怎么知道具体是那种情况呢?
其实我们也不知道,那就把这三种情况的答案都算出来,取其中结果最大的那个呗,因为题目让我们算「最长」公共子序列的长度嘛。
这三种情况的答案怎么算?回想一下我们的dp函数定义,不就是专门为了计算它们而设计的嘛!
代码可以再进一步:
// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
if (s1.charAt(i) == s2.charAt(j)) {
return 1 + dp(s1, i + 1, s2, j + 1)
} else {
// s1[i] 和 s2[j] 中至少有一个字符不在 lcs 中,
// 穷举三种情况的结果,取其中的最大结果
return max(
// 情况一、s1[i] 不在 lcs 中
dp(s1, i + 1, s2, j),
// 情况二、s2[j] 不在 lcs 中
dp(s1, i, s2, j + 1),
// 情况三、都不在 lcs 中
dp(s1, i + 1, s2, j + 1)
);
}
}
这里就已经非常接近我们的最终答案了,还有一个小的优化,情况三「s1[i]和s2[j]都不在 lcs 中」其实可以直接忽略。
因为我们在求最大值嘛,情况三在计算s1[i+1..]和s2[j+1..]的lcs长度,这个长度肯定是小于等于情况二s1[i..]和s2[j+1..]中的lcs长度的,因为s1[i+1..]比s1[i..]短嘛,那从这里面算出的lcs当然也不可能更长嘛。
同理,情况三的结果肯定也小于等于情况一。说白了,情况三被情况一和情况二包含了,所以我们可以直接忽略掉情况三,完整代码如下:
// 备忘录,消除重叠子问题
int[][] memo;
/* 主函数 */
int longestCommonSubsequence(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 备忘录值为 -1 代表未曾计算
memo = new int[m][n];
for (int[] row : memo)
Arrays.fill(row, -1);
// 计算 s1[0..] 和 s2[0..] 的 lcs 长度
return dp(s1, 0, s2, 0);
}
// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
// base case
if (i == s1.length() || j == s2.length()) {
return 0;
}
// 如果之前计算过,则直接返回备忘录中的答案
if (memo[i][j] != -1) {
return memo[i][j];
}
// 根据 s1[i] 和 s2[j] 的情况做选择
if (s1.charAt(i) == s2.charAt(j)) {
// s1[i] 和 s2[j] 必然在 lcs 中
memo[i][j] = 1 + dp(s1, i + 1, s2, j + 1);
} else {
// s1[i] 和 s2[j] 至少有一个不在 lcs 中
memo[i][j] = Math.max(
dp(s1, i + 1, s2, j),
dp(s1, i, s2, j + 1)
);
}
return memo[i][j];
}
以上思路完全就是按照我们之前的爆文 动态规划套路框架 来的,应该是很容易理解的。至于为什么要加memo备忘录,我们之前写过很多次,为了照顾新来的读者,这里再简单重复一下,首先抽象出我们核心dp函数的递归框架:
int dp(int i, int j) {
dp(i + 1, j + 1); // #1
dp(i, j + 1); // #2
dp(i + 1, j); // #3
}
你看,假设我想从dp(i, j)转移到dp(i+1, j+1),有不止一种方式,可以直接走#1,也可以走#2 -> #3,也可以走#3 -> #2。
这就是重叠子问题,如果我们不用memo备忘录消除子问题,那么dp(i+1, j+1)就会被多次计算,这是没有必要的。
至此,最长公共子序列问题就完全解决了,用的是自顶向下带备忘录的动态规划思路,我们当然也可以使用自底向上的迭代的动态规划思路,和我们的递归思路一样,关键是如何定义dp数组,
我这里也写一下自底向上的解法吧:
⚠️:大小加一的原因是,索引为零的位置代表空串


int longestCommonSubsequence(String s1, String s2) {
int m = s1.length(), n = s2.length();
int[][] dp = new int[m + 1][n + 1];
// 定义:s1[0..i-1] 和 s2[0..j-1] 的 lcs 长度为 dp[i][j]
// 目标:s1[0..m-1] 和 s2[0..n-1] 的 lcs 长度,即 dp[m][n]
// base case: dp[0][..] = dp[..][0] = 0
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 现在 i 和 j 从 1 开始,所以要减一
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
// s1[i-1] 和 s2[j-1] 必然在 lcs 中
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
// s1[i-1] 和 s2[j-1] 至少有一个不在 lcs 中
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[m][n];
}
自底向上的解法中dp数组定义的方式和我们的递归解法有一点差异,而且由于数组索引从 0 开始,有索引偏移,不过思路和我们的递归解法完全相同,如果你看懂了递归解法,这个解法应该不难理解。
另外,自底向上的解法可以通过我们前文讲过的 动态规划状态压缩技巧 来进行优化,把空间复杂度压缩为 O(N),这里由于篇幅所限,就不展开了。
#1160. 拼写单词
- Easy
- 2019.08.30:😭
题目:
给你一份『词汇表』(字符串数组) words 和一张『字母表』(字符串) chars。
假如你可以用 chars 中的『字母』(字符)拼写出 words 中的某个『单词』(字符串),那么我们就认为你掌握了这个单词。
注意:每次拼写(指拼写词汇表中的一个单词)时,chars 中的每个字母都只能用一次。
返回词汇表 words 中你掌握的所有单词的 长度之和。
示例 1:
输入:words = ["cat","bt","hat","tree"], chars = "atach"
输出:6
解释:
可以形成字符串 "cat" 和 "hat",所以答案是 3 + 3 = 6。
分析:
这是一类经典的题型。凡是和“变位词”、“字母顺序打乱”相关的题目,都考虑统计字母出现的次数。这种方法我叫做 “counter 方法”。
我们既统计“字母表”中字母出现的次数,也统计单词中字母出现的次数。如果单词中每种字母出现的次数都小于等于字母表中字母出现的次数,那么这个单词就可以由字母表拼出来。
如何实现计数结构呢?一般的方法是用 Java 的 HashMap。但是我们注意到题目有一个额外的条件:所有字符串中都仅包含小写英文字母。这意味着我们可以用一个长度为 26 的数组来进行计数。

代码:
public int countCharacters(String[] words, String chars) {
int[] chars_count = count(chars); // 统计字母表的字母出现次数
int res = 0; // 所有可用单词长度之和
for (String word : words) {
int[] word_count = count(word); // 统计单词的字母出现次数
if (contains(chars_count, word_count)) {
res += word.length();
}
}
return res;
}
// 检查字母表的字母出现次数是否覆盖单词的字母出现次数
boolean contains(int[] chars_count, int[] word_count) {
for (int i = 0; i < 26; i++) {
if (chars_count[i] < word_count[i]) {
return false;
}
}
return true;
}
// 统计 26 个字母出现的次数,用一个26位的数组表示
int[] count(String word) {
int[] counter = new int[26];
for (int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
counter[c-'a']++;
}
return counter;
}
#1371. 每个元音包含偶数次的最长子字符串
- 中等
- 2021.04.13:
题目:
给你一个字符串 s ,请你返回满足以下条件的最长子字符串的长度:每个元音字母,即 'a','e','i','o','u' ,在子字符串中都恰好出现了偶数次。
示例 1:
输入:s = "eleetminicoworoep"
输出:13
解释:最长子字符串是 "leetminicowor" ,它包含 e,i,o 各 2 个,以及 0 个 a,u 。
示例 2:
输入:s = "leetcodeisgreat"
输出:5
解释:最长子字符串是 "leetc" ,其中包含 2 个 e 。
分析:前缀和 + 状态压缩
首先排除暴力法(枚举所有子串)。
使用前缀和优化统计子串的时间复杂度:
对于每个子串,都对应着一个区间。如果想要在不遍历重复子串的前提下快去求出该区间内元音字母出现的次数,就可以考虑使用前缀和。
对于每个元音字母都维护一个前缀和,定义pre[i][k]表示在字符串前i个字符中,第k个元音字母一共出现的次数。
之后对于一个区间,我们都可以用两个前缀和的差值来得到某个字母出现的次数。假设我们需要求出[left,right]这个区间的子串是否满足条件,那么我们可以用pre[right][k]-pre[left-1][k]在O(1)的时间复杂度下得到第k个元音字母出现的次数。注意对于每一个元音字母都需要判断一下是否出现偶数次。

但是!虽然我们使用了前缀和优化了统计子串的时间复杂度,然而我们枚举所有子串的复杂度仍然需要O(n^2)。为了避免枚举所有子串,我们考虑枚举字符串的每个位置i,计算以它结尾的满足条件的最长字符串长度。即快速找到最小的$j∈[0,i)$,满足pre[i][k]-pre[j][k](区间[j+1,i]每一个元音字母出现的次数)均为偶数,那么以i结尾的最长字符串s[j+1,i]长度就是i-j。
如何优化?正片开始:
考虑利用哈希表来优化查找的复杂度,但是单单利用前缀和,我们无法找到 i 和 j 相关的恒等式,像「1248. 统计优美子数组」这道题我们是能明确知道两个前缀的差值是恒定的。
这道题我们还有一个性质没有充分利用:我们需要找的子串中,每个元音字母都恰好出现了偶数次。
偶数这个条件其实告诉了我们,对于满足条件的子串而言,两个前缀和pre[i][k]和pre[j][k]的奇偶性一定是相同的,因为小学数学的知识告诉我们:奇数减奇数等于偶数,偶数减偶数等于偶数。因此我们可以对前缀和稍作修改,从维护元音字母出现的次数改作维护元音字母出现次数的奇偶性。
⭐️ 那么 s[j+1,i]满足条件当且仅当对于所有的 k,pre[i][k]和pre[j][k] 的奇偶性都相等,此时我们就可以利用哈希表存储每一种奇偶性(即考虑所有的元音字母)对应最早出现的位置,边遍历边更新答案。(如果子串 [0,i] 与字串 [0,j] 状态相同,那么字串 [j+1,i] 的状态一定是 00000,因此可以记录每个状态第一次出现的位置,此后再出现该状态时相减即可。)
进阶
题目做到这里基本上做完了,但是我们还可以进一步优化我们的编码方式,如果直接以每个元音字母出现次数的奇偶性为哈希表中的键(如下),难免有些冗余,我们可能需要额外定义一个状态:
{
a: cnta, // a 出现次数的奇偶性
e: cnte, // e 出现次数的奇偶性
i: cnti, // i 出现次数的奇偶性
o: cnto, // o 出现次数的奇偶性
u: cntu // u 出现次数的奇偶性
}
将这么一个结构当作我们哈希表存储的键值,如果题目稍作修改扩大了字符集,那么维护起来可能会比较吃力。考虑到出现次数的奇偶性其实无非就两个值,0 代表出现了偶数次,1 代表出现了奇数次,我们可以将其压缩到一个二进制数中,第 k 位的 1 或 0 代表了第 k 个元音字母出现的奇偶性。
举一个例子,假如到第 i 个位置, o e u e a 出现的奇偶性分别为 1 1 0 0 1,那么我们就可以将其压成一个二进制数 11001,即十进制的 25 作为它的状态。这样我们就可以将 5 个元音字母出现次数的奇偶性压缩到了一个二进制数中,且连续对应了二进制数[00000,11111] 的范围,转成十进制数即[0,31]。因此我们也不再需要使用哈希表,直接用一个长度为 32 的数组来存储对应状态出现的最早位置即可。
🤔️pos[status] = i + 1 表示当前串长度为i+1时各个元音字母的状态.为什么记录的数组要赋值 i+1,而不是当前的位置 i ?其实很简单,因为如果最后的子串是从第一个字符开始的,就会出现长度少了1的情况。例如输入bbb,由于都不是元音,因此前缀和都是0,最长子串就是这个字符串本身,如果存储的是当前位置 i,那结果就是 2-0=2. 只能输出2,所以这里需要存储当前字符串长度。
举个例子:
- 如字符串
leetcode,状态00000第一次出现在空串(i=0)中,该状态最后一次出现则是子串leetc(i=4)中,如果status对应的pos[status]大于等于0(即不等于初始值-1),说明已经找到符合要求的子串。因为两个子串的奇偶性相等,说明中间子串是符合要求的,即它们中间必定出现了偶数次数的aeiou。所以长度为4-0+1=5 - 如字符串
bbb,状态00000第一次出现在空串(i=0)中,该状态最后一次出现则是子串bbb(i=2)中,所以长度为2-0+1=3
代码:
public int findTheLongestSubstring(String s) {
//pos数组存储的是元音字母每种奇偶状态第一次出现时数组的下标
//五个元音字母有从00000-11111一共32种状态,0代表偶数,1代表奇数,
int[] pos = new int[1 << 5]; //1左移5次 相当于2^5=32
//把数组用-1填充,区分00000的情况
Arrays.fill(pos, -1);
int res = 0;
int status = 0; //⭐️status对应的是当前节点所有元音字母的奇偶性
pos[0] = 0; //状态00000第一次出现在字符串长度为0的时候,这么设置是为了配合i+1
//有n个字符 循环n次,状态值初始为0
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (ch == 'a') {
status ^= (1 << 0); //与1异或,相同为0,不同为1
} else if (ch == 'e') {
status ^= (1 << 1);
} else if (ch == 'u') {
status ^= (1 << 2);
} else if (ch == 'i') {
status ^= (1 << 3);
} else if (ch == 'o') {
status ^= (1 << 4);
}
//如果status对应的pos[status]不等于初始值-1了 说明已经找到符合要求的子串
//因为两个子串的奇偶性相等,说明中间子串是符合要求的。
//奇偶性相同的两个数的差,必定为偶数 只会有一个偶数00000
//因此出现两个相同状态的数,他们中间必定出现了偶数次数的aeiou
if (pos[status] != -1) {
res = Math.max(res, i + 1 - pos[status]);
} else {
//pos[status]==-1 说明该status是第一次出现,只保存最先出现的这个值
pos[status] = i + 1; // 表示在字符串长度为i时,各个元音字母的状态。即pos[状态]=第一次出现该状态时当前串的长度
}
}
return res;
}
字符串乘法计算
- 中等
- 2021.04.11:😭
题目:
给定两个以字符串形式表示的非负整数 numl和 num2,返回numl 和 num2的乘积,它们的乘积也表示为字符串形式。
示例:
输入: num1 = "123", num2 = "456"
输出: "56088"
分析:
对于比较小的数字,做运算可以直接使用编程语言提供的运算符,但是如果相乘的两个因数非常大,语言提供的数据类型可能就会溢出。
需要注意的是,num1和num2可以非常长,所以不可以把他们直接转成整型然后运算,唯一的思路就是模仿我们手算乘法。
比如说我们手算123 × 45,应该会这样计算,有两个指针i,j在num1和num2上游走,计算乘积,同时将乘积叠加到res的正确位置:
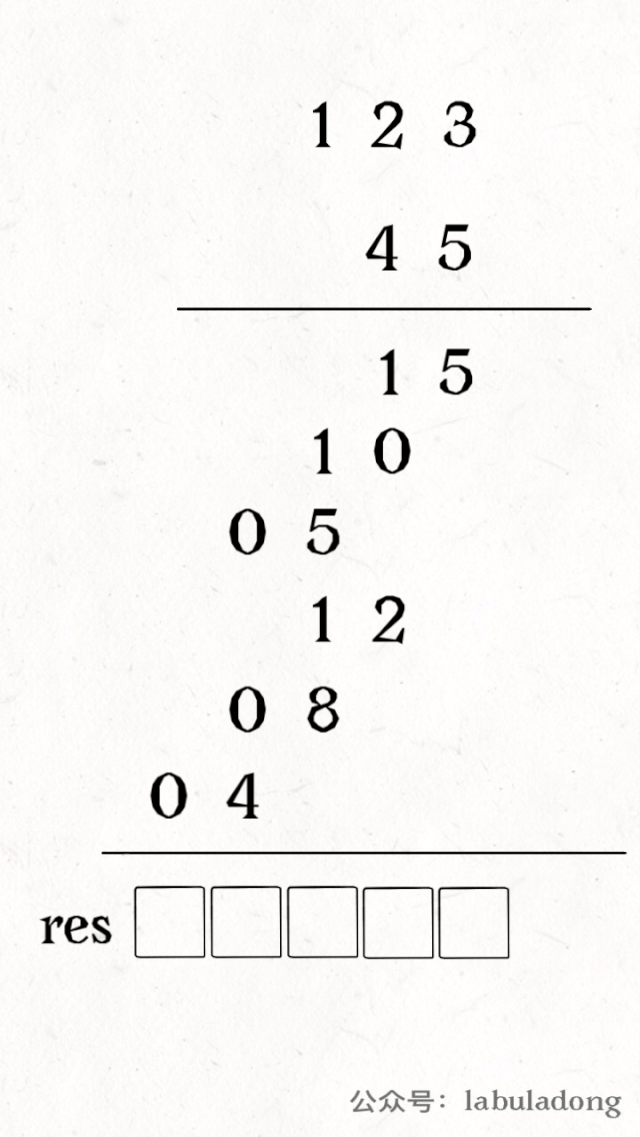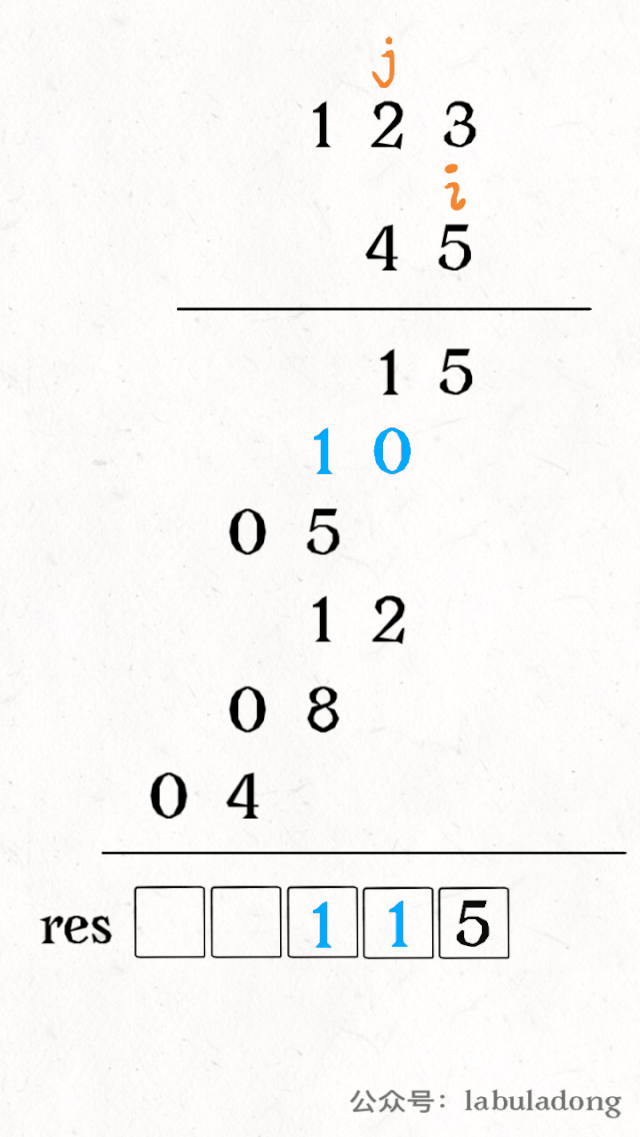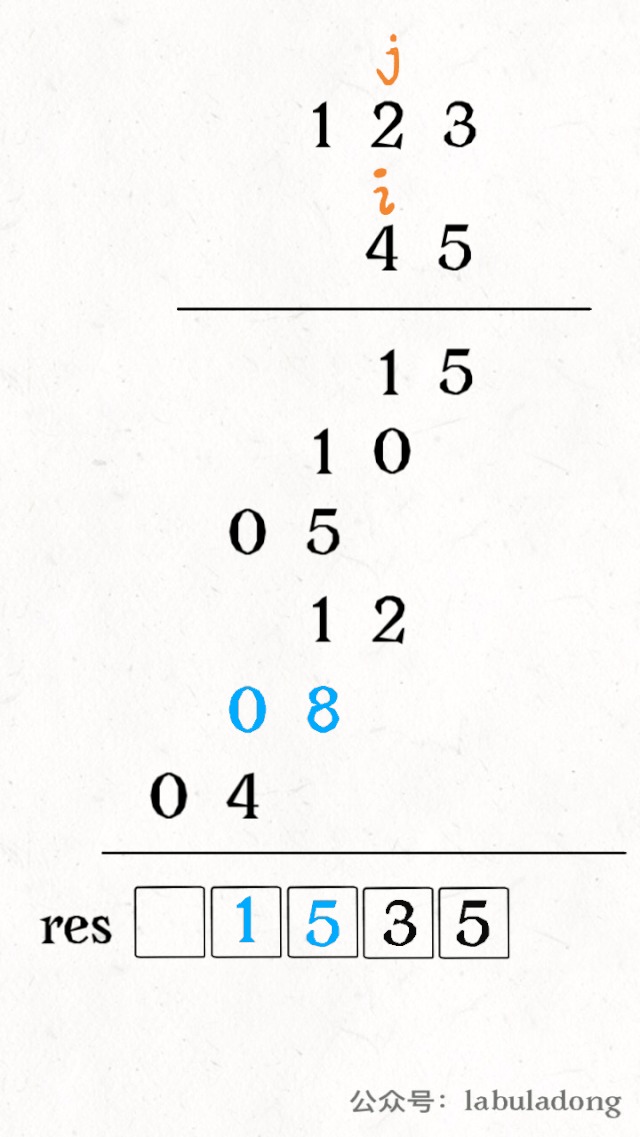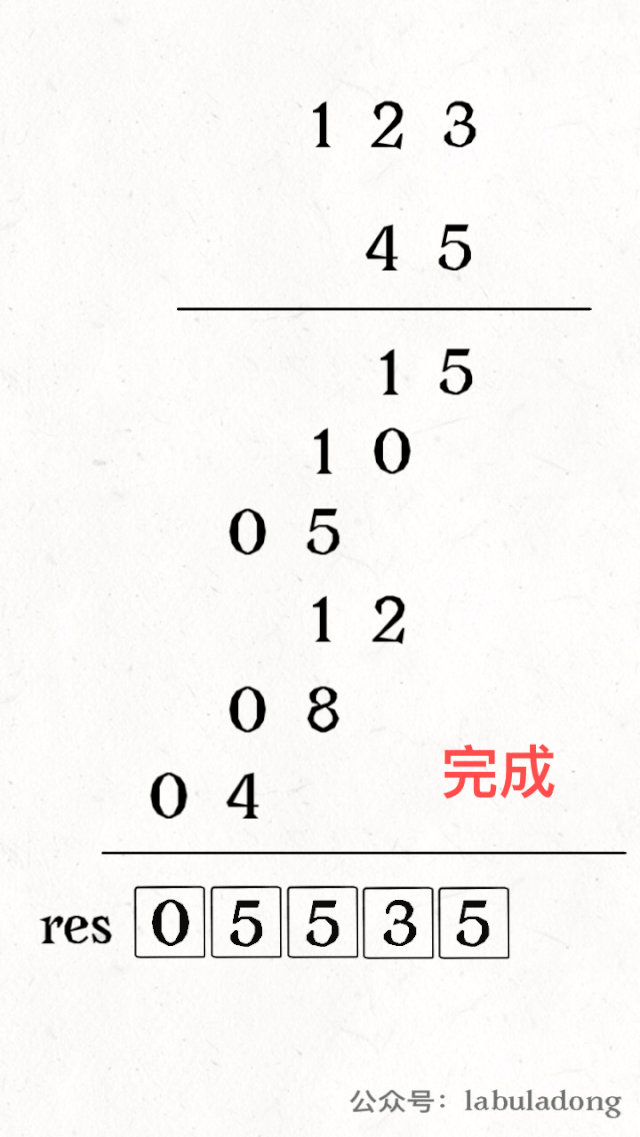
现在还有一个关键问题,如何将乘积叠加到res的正确位置,或者说,如何通过i,j计算res的对应索引呢?
其实,细心观察之后就发现,num1[i]和num2[j]的乘积对应的就是res[i+j]和res[i+j+1]这两个位置。
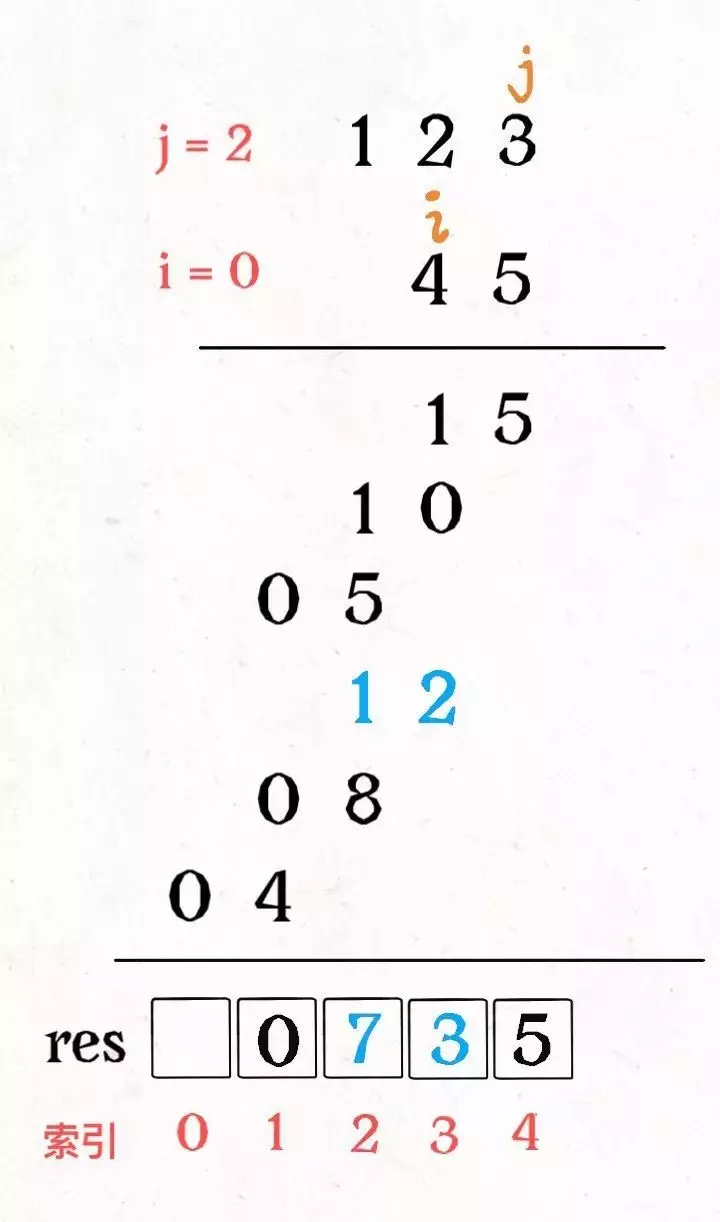
代码:
private String multiply(String num1,String num2){
// 结果最多为 m+n 位数
int m = num1.length();
int n = num2.length();
int[] res = new int[m+n];
// 从个位开始逐位相乘
for (int i = m-1; i >=0 ; i--) {
for (int j = n-1; j >=0 ; j--) {
int mul = (num1.charAt(i)-'0') * (num2.charAt(j)-'0');
// 乘积在 res 对应的索引位置
int p1 = i+j;
int p2 = i+j+1;
// 叠加到 res 上
int sum = mul+res[p2]; // 因为可能会发生进位,所以先加上最末尾位的当前值
res[p2] = sum%10;
res[p1] += sum/10;
}
}
// 结果前缀可能存的0 (未使用的位)
int prefix = 0;
while (prefix<res.length&&res[prefix]==0){
prefix++;
}
// 将计算结果转化为字符串
StringBuilder builder = new StringBuilder();
int zeroIndex = Integer.MAX_VALUE;
for (int i = 0; i < res.length; i++) {
builder.append(res[i]);
if (res[i]==0&&i<zeroIndex){
zeroIndex = i;
}
}
return builder.toString().substring(zeroIndex+1,res.length);
}
手写生产者消费者
- wait() / notify()方法
- await() / signal()方法
- BlockingQueue阻塞队列方法
// wait() / notify()方法
public static void main(String args[]) {
Storage storage = new Storage();
new Thread(storage::produce, "生产者P1").start();
new Thread(storage::produce, "生产者P2").start();
new Thread(storage::produce, "生产者P3").start();
new Thread(storage::consume, "消费者C1").start();
new Thread(storage::consume, "消费者C2").start();
new Thread(storage::consume, "消费者C3").start();
}
/**
* 仓库/资源类
*/
public static class Storage {
// 设置队列缓存的大小。生产过程中超过这个大小就暂时停止生产
private int CAPACITY = 5;
// 仓库存储的载体
private Queue<String> queue = new LinkedList<>();
public synchronized void produce() {
int i = 0;
while (true) {
while (queue.size() == CAPACITY) {
try {
System.out.println("仓库已满,["+Thread.currentThread().getName()+"]等待消费者消费 ");
this.wait();
} catch (Exception ex) {
ex.printStackTrace();
}
}
System.out.println("[" + Thread.currentThread().getName() + "] 生产了 : +" + i);
queue.offer(i++ + "(由" + Thread.currentThread().getName() + "生产)");
this.notifyAll();
try {
TimeUnit.MILLISECONDS.sleep(new Random().nextInt(1000));
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
public synchronized void consume() {
while (true) {
while (queue.isEmpty()) {
try {
System.out.println("仓库空了,["+Thread.currentThread().getName()+"]等待生产");
this.wait();
} catch (Exception ex) {
ex.printStackTrace();
}
}
String s = queue.poll();
System.out.println("[" + Thread.currentThread().getName() + "] 消费了 : " + s);
this.notifyAll();
try {
TimeUnit.MILLISECONDS.sleep(new Random().nextInt(100));
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}
// await() / signal()方法
public static void main(String args[]) {
Storage storage = new Storage();
new Thread(storage::produce, "生产者P1").start();
new Thread(storage::produce, "生产者P2").start();
new Thread(storage::produce, "生产者P3").start();
new Thread(storage::consume, "消费者C1").start();
new Thread(storage::consume, "消费者C2").start();
new Thread(storage::consume, "消费者C3").start();
}
/**
* 仓库/资源类
*/
public static class Storage {
// 设置队列缓存的大小。生产过程中超过这个大小就暂时停止生产
private int CAPACITY = 5;
// 仓库存储的载体
private Queue<String> queue = new LinkedList<>();
private ReentrantLock lock = new ReentrantLock();
private Condition fullCondition = lock.newCondition();
private Condition emptyCondition = lock.newCondition();
public void produce() {
int i = 0;
while (true) {
lock.lock();
try {
while (queue.size() == CAPACITY) {
try {
System.out.println("仓库已满,["+Thread.currentThread().getName()+"]等待消费者消费 ");
fullCondition.await();
} catch (Exception ex) {
ex.printStackTrace();
}
}
System.out.println("[" + Thread.currentThread().getName() + "] 生产了 : +" + i);
queue.offer(i++ + "(由" + Thread.currentThread().getName() + "生产)");
// 唤醒其他所有生产者、消费者
fullCondition.signalAll();
emptyCondition.signalAll();
} catch (Exception e) {
e.printStackTrace();
} finally {
lock.unlock();
try {
TimeUnit.MILLISECONDS.sleep(new Random().nextInt(2000));
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}
public void consume() {
while (true) {
lock.lock();
try {
while (queue.isEmpty()) {
try {
System.out.println("仓库空了,["+Thread.currentThread().getName()+"]等待生产");
emptyCondition.await();
} catch (Exception ex) {
ex.printStackTrace();
}
}
String s = queue.poll();
System.out.println("[" + Thread.currentThread().getName() + "] 消费了 : " + s);
//唤醒其他所有生产者、消费者
fullCondition.signalAll();
emptyCondition.signalAll();
} catch (Exception e) {
e.printStackTrace();
} finally {
lock.unlock();
try {
TimeUnit.MILLISECONDS.sleep(new Random().nextInt(2000));
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}
}
// 阻塞队列
public static void main(String args[]) {
Storage storage = new Storage();
new Thread(storage::produce, "生产者P1").start();
new Thread(storage::produce, "生产者P2").start();
new Thread(storage::produce, "生产者P3").start();
new Thread(storage::consume, "消费者C1").start();
new Thread(storage::consume, "消费者C2").start();
new Thread(storage::consume, "消费者C3").start();
}
/**
* 仓库/资源类
*/
public static class Storage {
// 设置队列缓存的大小。生产过程中超过这个大小就暂时停止生产
private int CAPACITY = 5;
// 仓库存储的载体
private LinkedBlockingQueue<String> blockingQueue = new LinkedBlockingQueue<>(CAPACITY);
public void produce() {
int i = 0;
while (true) {
try {
blockingQueue.put(i++ + "(由" + Thread.currentThread().getName() + "生产)");
System.out.println(blockingQueue.size());
Thread.sleep(new Random().nextInt(1000));
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
public void consume() {
while (true) {
try {
String s = blockingQueue.take();
System.out.println("[" + Thread.currentThread().getName() + "] Consuming : " + s);
//暂停最多1秒
Thread.sleep(new Random().nextInt(1000));
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
}
手写阻塞队列
public static void main(String[] args) {
MyBlockingQueue myBlockingQueue = new MyBlockingQueue();
new Thread(()->{
for (int i = 0; i < 20; i++) {
myBlockingQueue.offer(i);
}
}).start();
new Thread(()->{
for (int i = 0; i < 20; i++) {
System.out.println(myBlockingQueue.poll());
}
}).start();
}
static class MyBlockingQueue{
private int capcity = 10;
private Queue<Integer> queue = new LinkedList<>();
public synchronized void offer(Integer i){
while (queue.size()==capcity){
try {
System.out.println("队列已满,等待插入: "+i);
this.wait();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
queue.offer(i);
System.out.println("数据插入成功: "+i);
this.notifyAll();
}
public synchronized Integer poll(){
while(queue.size()==0){
try {
System.out.println("队列为空!!");
this.wait();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
Integer listNode = queue.poll();
this.notifyAll();
return listNode;
}
}
线程轮流打印
三个线程轮流打印1A 2B 3C(三种方法),执行2轮。 多线程轮流执行用什么锁
总纲领:
-
高内聚低耦合前提下,线程操作资源类
-
判断/干活/通知
-
多线程交互中,必须要防止多线程的虚假唤醒,也即(判断只用while,不能用if)
// 主函数 线程操作资源类
public static void main(String[] args) {
ShareResource shareResource = new ShareResource();
new Thread(() -> {
for (int i = 0; i < 2; i++) {
shareResource.printA();
}
}, "A").start();
new Thread(() -> {
for (int i = 0; i < 2; i++) {
shareResource.printB();
}
}, "B").start();
new Thread(() -> {
for (int i = 0; i < 2; i++) {
shareResource.printC();
}
}, "C").start();
}
资源类的4种写法:
synchronized (Object的wait和notifyAll)
static class ShareResource {
private int number = 1; // A 1 B 2 c 3
public synchronized void printA() throws InterruptedException {
// 判断
while (number!=1){
this.wait();
}
// 干活
System.out.println("A");
// 通知
number = 2;
this.notifyAll();
}
public synchronized void printB() throws InterruptedException {
// 判断
while (number!=2){
this.wait();
}
// 干活
System.out.println("B");
// 通知
number = 3;
this.notifyAll();
}
public synchronized void printC() throws InterruptedException {
// 判断
while (number!=3){
this.wait();
}
// 干活
System.out.println("C");
// 通知
number = 1;
this.notifyAll();
}
}
ReentrantLock + condition (await/signal)
static class ShareResource {
private int number = 1; // A 1 B 2 c 3
private ReentrantLock lock = new ReentrantLock();
private Condition conditionA = lock.newCondition();
private Condition conditionB = lock.newCondition();
private Condition conditionC = lock.newCondition();
public void printA() {
lock.lock();
try {
// 1判断 2干活 3通知
while (number!=1){
conditionA.await();
}
System.out.println("A");
number=2;
conditionB.signal();
} catch (Exception e) {
e.printStackTrace();
} finally {
lock.unlock();
}
}
public void printB() {
lock.lock();
try {
// 1判断 2干活 3通知
while (number!=2){
conditionB.await();
}
System.out.println("B");
number=3;
conditionC.signal();
} catch (Exception e) {
e.printStackTrace();
} finally {
lock.unlock();
}
}
public void printC() {
lock.lock();
try {
// 1判断 2干活 3通知
while (number!=3){
conditionC.await();
}
System.out.println("C");
number=1;
conditionA.signal();
} catch (Exception e) {
e.printStackTrace();
} finally {
lock.unlock();
}
}
}
LockSupport(park/unpark)
static Thread t1 = null;
static Thread t2 = null;
static Thread t3 = null;
// 线程操作资源类 判断干活通知
static class ShareResource {
private int number = 1; // A 1 B 2 c 3
public void printA() throws InterruptedException {
// 判断
while (number!=1){
LockSupport.park();
}
// 干活
System.out.println("A");
// 通知
number = 2;
}
public void printB() throws InterruptedException {
// 判断
while (number!=2){
LockSupport.park();
}
// 干活
System.out.println("B");
// 通知
number = 3;
}
public void printC() throws InterruptedException {
// 判断
while (number!=3){
LockSupport.park();
}
// 干活
System.out.println("C");
// 通知
number = 1;
}
}
public static void main(String[] args) {
ShareResource shareResource = new ShareResource();
t1=new Thread(() -> {
for (int i = 0; i < 2; i++) {
try {
shareResource.printA();
LockSupport.unpark(t2);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}, "A");
t2 = new Thread(() -> {
for (int i = 0; i < 2; i++) {
try {
shareResource.printB();
LockSupport.unpark(t3);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}, "B");
t3=new Thread(() -> {
for (int i = 0; i < 2; i++) {
try {
shareResource.printC();
LockSupport.unpark(t1);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}, "C");
t1.start();
t2.start();
t3.start();
}
信号量Semaphore
static class ShareResource {
private Semaphore semaphoreA = new Semaphore(1);
private Semaphore semaphoreB = new Semaphore(0);
private Semaphore semaphoreC = new Semaphore(0);
public void printA() throws InterruptedException {
semaphoreA.acquire();
System.out.println("A");
semaphoreB.release();
}
public void printB() throws InterruptedException {
semaphoreB.acquire();
System.out.println("B");
semaphoreC.release();
}
public void printC() throws InterruptedException {
semaphoreC.acquire();
System.out.println("C");
semaphoreA.release();
}
}
IP地址与整数的相互转换
ip转整数 把IP地址转换成INT型存储
- 通过String的split方法按.分隔得到4个长度的数组
- 通过左移位操作(«)给每一段的数字加权,第一段的权为2的24次方,第二段的权为2的16次方,第三段的权为2的8次方,最后一段的权为1
public static long ipToLong(String strIp) {
String[] ip = strIp.split("\\.");
return (Long.parseLong(ip[0]) << 24)
+ (Long.parseLong(ip[1]) << 16) + (Long.parseLong(ip[2]) << 8) + Long.parseLong(ip[3]);
}
将数值转换为ip地址
- 将整数值进行右移位操作(»>),右移24位,右移时高位补0,得到的数字即为第一段IP。
- 通过与操作符(&)将整数值的高8位设为0,再右移16位,得到的数字即为第二段IP。
- 通过与操作符吧整数值的高16位设为0,再右移8位,得到的数字即为第三段IP。
- 通过与操作符吧整数值的高24位设为0,得到的数字即为第四段IP。
public static String longToIP(Long longIP) {
StringBuilder builder = new StringBuilder();
builder.append((longIP>>>24)+"."); // 直接右移24位
builder.append(((longIP&0x00FFFFFF)>>>16)+"."); // 将高8位置0,然后右移16位
builder.append(((longIP&0x0000FFFF)>>>8)+"."); // 将高16位置0,然后右移8位
builder.append((longIP&0x000000FF)); // 将高24位置0
return builder.toString();
}
大数求和
- 思路一:定义String变量str1和str2分别存储输入的两个大数,定义num1[]和num2[]两个int型数组,将两个字符串分别逐个字符逆序存入数组(因为要从后面加起),定义sum[]数组存放求和结果,使用循环两个数组中的元素逐位相加,并判断是否进位,最后逆序输出数组sum[]中的每个元素。
- 思路二,使用栈结构实现将输入的数字依次存进栈中(栈有先进后出的特点,所以先输入的高位上的数字会被存在栈的底层),在计算和的时候从两个栈中依次取出数据相加存入新的栈中(计算时在栈顶的是个位,然后是十位,以此类推,存进新的栈时在栈底的是个位,然后是十位,以此类推),最后将存放计算结果的栈中元素自顶向底取出打印,这种方法效率较高,时间复杂度低,但是空间复杂度很大,需要占用较多的空间资源。
// 方式一
private String largeIntegerSum(String numA, String numB) {
int lenA = numA.length();
int lenB = numB.length();
int maxLen = Math.max(lenA, lenB)+1; // 多一位,因为可能会进位
int[] arrayA = new int[maxLen];
int[] arrayB = new int[maxLen];
int[] result = new int[maxLen];
// 将字符串逆序存储到数组中
for (int i = 0; i < lenA; i++) {
arrayA[i] = numA.charAt(lenA-i-1)-'0';
}
for (int i = 0; i < lenB; i++) {
arrayB[i] = numB.charAt(lenB-i-1)-'0';
}
// 进行大数求和
for (int i = 0; i < maxLen; i++) {
int add = result[i]+ arrayA[i]+arrayB[i];
if (add<10){ // 没有进位
result[i] = add;
}else { // 有进位
int remainder = add%10; // 余数
result[i] = remainder;
// 放置进位,注意防止越界
if (i!=maxLen-1){
result[i+1] = 1;
}
}
}
// 再将数组逆序得到最终的结果,先去掉末尾的0
StringBuilder builder = new StringBuilder();
int lastIndex = 0;
for (int i = maxLen-1; i >=0 ; i--) {
if (result[i]!=0){
lastIndex = i;
break;
}
}
for (int i = lastIndex; i >=0 ; i--) {
builder.append(result[i]);
}
return builder.toString();
}
// 方式二
private String largeIntegerSum(String numA, String numB) {
// 将两数放入栈中
Stack<Integer> stackA = new Stack<>();
Stack<Integer> stackB = new Stack<>();
Stack<Integer> res = new Stack<>(); // 存放结果和
for (int i = 0; i < numA.length(); i++) {
stackA.push(numA.charAt(i)-'0');
}
for (int i = 0; i < numB.length(); i++) {
stackB.push(numB.charAt(i)-'0');
}
int c = 0; // 进位标志位
// 求和
while (!stackA.isEmpty()&&!stackB.isEmpty()){
int add = c + stackA.pop() + stackB.pop();
if (add<10){
res.push(add);
c = 0;
}else {
res.push(add%10);
c = 1;
}
}
// 继续加上不为空的栈
Stack<Integer> remain = stackA.isEmpty()?stackB:stackA;
while (!remain.isEmpty()){
int add = c + remain.pop();
if (add<10){
res.push(add);
c = 0;
}else {
res.push(add%10);
c = 1;
}
}
// 最高位有进位时,直接最后一个数为1
if (c==1){
res.push(1);
}
// 返回结果
StringBuilder builder = new StringBuilder();
while (!res.isEmpty()){
builder.append(res.pop());
}
return builder.toString();
}
n!末尾0的个数
- 简单
- 2021.04.13:
题目:
输入一个正整数n,求 n! 末尾有多少个0;
实例:
n = 10 时, n! = 3628800,所以答案为2
分析:
10进制数结尾的每一个0都表示有一个因数10存在——任何进制都一样,对于一个M进制的数,让结尾多一个0就等价于乘以M。
10可以分解为2 × 5——因此只有质数2和5相乘能产生0,别的任何两个质数相乘都不能产生0,而且2,5相乘只产生一个0。
所以,分解后的整个因数式中有多少对(2, 5),结果中就有多少个0,而分解的结果中,2的个数显然是多于5的,因此,有多少个5,就有多少个(2, 5)对。
所以,讨论1000的阶乘结尾有几个0的问题,就被转换成了1到1000所有这些数的质因数分解式有多少个5的问题。
代码:
public int getResult(int n){
if (n<5) return 0;
int count = 0;
for (int i = 5; i <= n; i++) {
int temp = i;
while (temp/5!=0&&temp%5==0){
temp = temp/5;
count++;
}
}
return count;
}
判定子序列
- 简单
- 2021.04.13:
题目:
如何判定字符串s是否是字符串t的子序列(可以假定s长度比较小,且t的长度非常大)。举两个例子:
s = "abc", t = "ahbgdc", return true.
s = "axc", t = "ahbgdc", return false.
分析:
方法一: 双指针
其思路也非常简单,利用双指针i, j分别指向s, t,一边前进一边匹配子序列
方法二: 二分查找
这不就是最优解法了吗,时间复杂度只需 O(N),N 为t的长度。
是的,如果仅仅是这个问题,这个解法就够好了,不过这个问题还有 后续:
如果给你一系列字符串s1,s2,...和字符串t,你需要判定每个串s是否是t的子序列(可以假定s相对较短,t很长)。
boolean[] isSubsequence(String[] sn, String t);
你也许会问,这不是很简单吗,还是刚才的逻辑,加个 for 循环不就行了?
可以,但是此解法处理每个s时间复杂度仍然是 O(N),而如果巧妙运用二分查找,可以将时间复杂度降低,大约是 O(MlogN),M 为 s 的长度。由于 N 相对 M 大很多,所以后者效率会更高。
二分思路主要是对t进行预处理,用一个字典index将每个字符出现的索引位置按顺序存储下来(对于 ASCII 字符,可以用大小为 256 的数组充当字典):
二分查找返回目标值val的索引,对于搜索左侧边界的二分查找,有一个特殊性质:当val不存在时,得到的索引恰好是比val大的最小元素索引。

代码:
// 双指针
private boolean isSubsequence(String str1, String str2) {
int i = 0, j = 0;
while (i < str1.length() && j < str2.length()) {
if (str1.charAt(i) == str2.charAt(j)) {
i++;
}
j++;
}
return i == str1.length();
}
// 方法二:建立索引+二分查找
private boolean isSubsequence(String str1, String str2) {
// 预处理 建立索引
ArrayList<Integer>[] index = new ArrayList[256];
for (int i = 0; i < str2.length(); i++) {
char c = str2.charAt(i);
if (index[c]==null){
index[c] = new ArrayList<>();
}
index[c].add(i);
}
// 串t上的指针
int j = 0;
// 借助 index 查找 s[i]
for (int i = 0; i < str1.length(); i++) {
char c = str1.charAt(i);
// 不包含字符c
if (index[c]==null) return false;
// 二分查找区间中未找到字符c
int pos = leftBinarySearch(index[c],j);
if (pos==-1) return false;
// 变更j为最新的索引+1
j = index[c].get(pos)+1;
}
return true;
}
// 当target不存在时,得到的索引恰好是比target大的最小元素索引
private int leftBinarySearch(ArrayList<Integer> arr, int target) {
int left = 0;
int right = arr.size()-1;
while (left<=right){
int mid = left + (right-left)/2;
if (target>arr.get(mid)){
left = mid +1;
}else if (target<arr.get(mid)){
right = mid-1;
}else if (target==arr.get(mid)){
right = mid-1;
}
}
if (left==arr.size()) return -1; // target 比所有元素都大
return left;
}
乘积最大
- 中等
- 2021.04.13:
题目:
设有一个长度为N的数字串,要求选手使用K个乘号将它分成K+1个部分,找出一种分法,使得这K+1个部分的乘积能够为最大。
同时,为了帮助选手能够正确理解题意,主持人还举了如下的一个例子:
有一个数字串:312, 当N=3,K=1时会有以下两种分法:
3*12=36
31*2=62
这时,符合题目要求的结果是:31*2=62
分析:⚠️:j<=m<i

举例:dp[2][1] = max(dp[2][1],dp[1][0]*mul[2][2]) = max(0,1*2) = 2; 2<=m<1
dp[3][1] = max(dp[3][1],dp[1][0]*mul[2][3],dp[2][0]*mul[3][3]) = max(0,1*23,12*3) = 36; 3<=m<1

代码:
public static int getResult(String str,int n){
char[] arr = str.toCharArray();
int len = str.length();
int[][] dp = new int[len][n+1];
// 初始化dp[i][0]:前i个字符有0个乘号时的最大值
for (int i = 0; i < str.length(); i++) {
for (int j = 0; j <= i; j++) {
dp[i][0] = dp[i][0]*10 +(arr[j]-'0');
}
}
// 状态转移 dp[i,j] = max(dp[i][j],dp[m,j-1]*mul[m+1,i]) j<=m<i
// mul[i][j]:字符串的第i位到第j位表示的数字
for (int j = 1; j < n + 1; j++) {
for (int i = len-1; i >= j; i--) {
// 取最大值
for (int m = j-1; m < i; m++) {
dp[i][j] = Math.max(dp[i][j],dp[m][j-1]*getMul(str,m+1,i));
}
}
}
return dp[len-1][n];
}
private static int getMul(String s,int start, int end) {
return Integer.parseInt(s.substring(start,end+1));
}
分段和最大值最小
- 中等
- 2021.09.10:
题目:
有一个长度为n的序列A,序列中的第i个数为A[i] (1<=i<=n),现在你可以将序列分成至多连续的k段。 对于每一段,我们定义这一段的不平衡度为段内的最大值减去段内的最小值。显然,对于长度为1的段,其不平衡度为0。 对于一种合法的分段方式(即每一段连续且不超过k段),我们定义这种分段方式的不平衡度为每一段的不平衡度的最大值。 现在你需要找到不平衡度最小的分段方式,输出这种分段方式的不平衡度即可。
如 3 3 5 5 2 5 至多分为3段
最终分为[3 5 5], [2], [5],该种分段方式的不平衡度为2。
分析:分段check
算出差值范围,用二分枚举差值大小,然后去模拟check
要求每段和最大值最小,left取这个数列中元素最小值,right取整个数列最大值和最小值的差值。那么要求的每段和的不平衡度的最大值就一定在left和right之间。可以再用二分法进行求解。
这种题目的关键在于理解好check()函数的意义。
check()函数中
代码:
public static int getResult(int[] nums, int k) {
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
// 首先找出整个数组中的两个最值
for (int num : nums) {
max = Math.max(max, num);
min = Math.min(min, num);
}
// 这里是采用了二分的思路,因为段的不平衡度是非严格递增的(有不变的情况,如12234),也就是有序的,故可以使用二分法
// left为0,即平衡度的最小值;right为max-min,即段为整个数组时的平衡度,此时拆分后的段的平衡度不可能超过这个值
int l = -1, r = max - min + 1, m = 0;
while (l + 1 != r) {
m = (l + r) / 2;
// 检查平衡度小于等于m的段是否存在,若不存在,说明需要往大于m的方向寻找
if (!check(nums, k, m)) {
l = m;
} else { // 若存在,我们缩小右边界,看看是否存在更小的平衡度
r = m;
}
}
// 因为left是从0开始的,而且每次只递增1,那么最后跳出时就是我们所求的结果
return r;
}
// 检查该平衡度下分段时候超出限制
static boolean check(int[] nums, int k, int x) {
int max = nums[0], min = nums[0];
for (int i = 1; i < nums.length; i++) {
max = Math.max(max, nums[i]);
min = Math.min(min, nums[i]);
// 当平衡度大于x时,开启下一个段。直到达到段数的限制,则返回false
if (max - min > x) {
k--;
if (k <= 0) {
return false;
}
max = min = nums[i];
}
}
return k > 0;
}
既已览卷至此,何不品评一二: